Score calculation
1. Score terminology
1.1. What is a score?
Every @PlanningSolution class has a score.
The score is an objective way to compare two solutions.
The solution with the higher score is better.
The Solver aims to find the solution with the highest Score of all possible solutions.
The best solution is the solution with the highest Score that Solver has encountered during solving,
which might be the optimal solution.
Timefold cannot automatically know which solution is best for your business,
so you need to tell it how to calculate the score of a given @PlanningSolution instance according to your business needs.
If you forget or are unable to implement an important business constraint, the solution is probably useless:
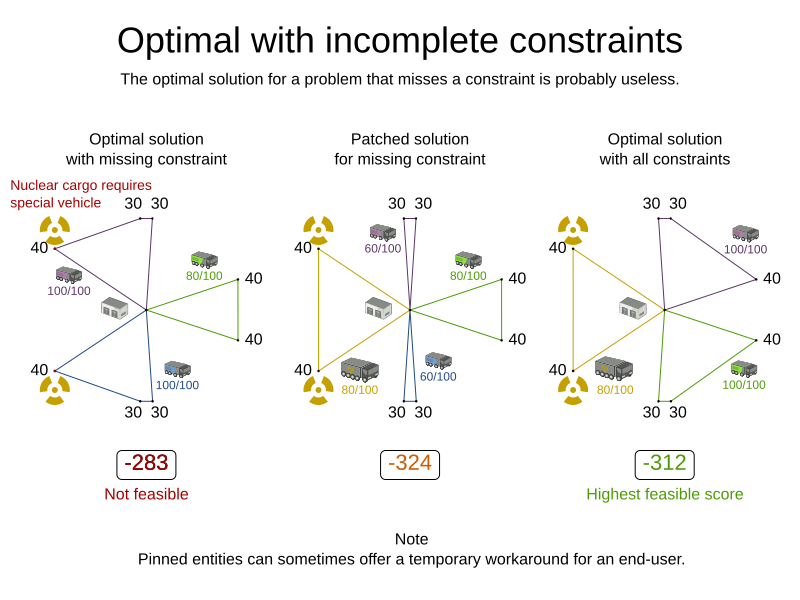
1.2. Formalize the business constraints
To implement a verbal business constraint, it needs to be formalized as a score constraint. Luckily, defining constraints in Timefold is very flexible through the following score techniques:
-
Score signum (positive or negative): maximize or minimize a constraint type
-
Score weight: put a cost/profit on a constraint type
-
Score level (hard, soft, …): prioritize a group of constraint types
-
Pareto scoring (rarely used)
Take the time to acquaint yourself with the first three techniques. Once you understand them, formalizing most business constraints becomes straightforward.
|
Do not presume that your business knows all its score constraints in advance. Expect score constraints to be added, changed or removed after the first releases. |
1.3. Score constraint signum (positive or negative)
All score techniques are based on constraints. A constraint can be a simple pattern (such as Maximize the apple harvest in the solution) or a more complex pattern. A positive constraint is a constraint you want to maximize. A negative constraint is a constraint you want to minimize
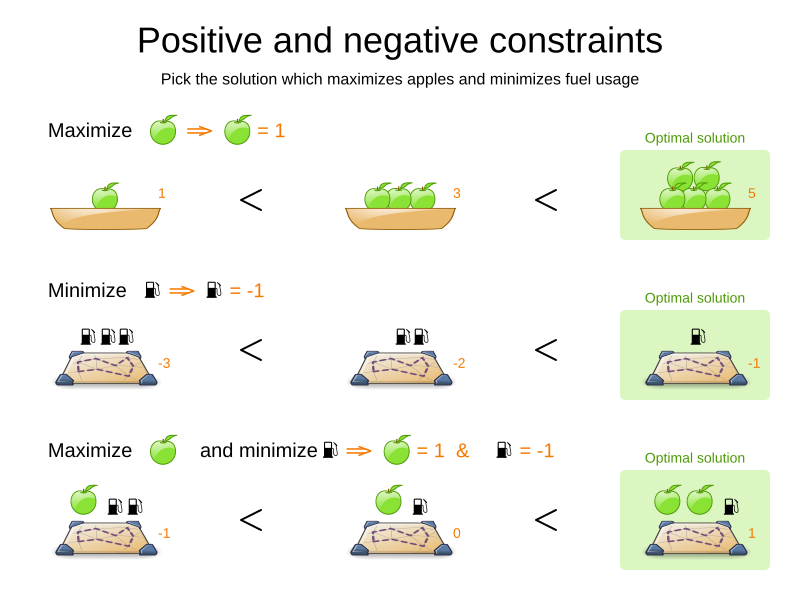
The image above illustrates that the optimal solution always has the highest score, regardless if the constraints are positive or negative.
Most planning problems have only negative constraints and therefore have a negative score. In that case, the score is the sum of the weight of the negative constraints being broken, with a perfect score of 0. For example in n queens, the score is the negative of the number of queen pairs which can attack each other.
Negative and positive constraints can be combined, even in the same score level.
When a constraint activates (because the negative constraint is broken or the positive constraint is fulfilled) on a certain planning entity set, it is called a constraint match.
1.4. Score constraint weight
Not all score constraints are equally important. If breaking one constraint is equally bad as breaking another constraint x times, then those two constraints have a different weight (but they are in the same score level). For example in vehicle routing, you can make one unhappy driver constraint match count as much as two fuel tank usage constraint matches:
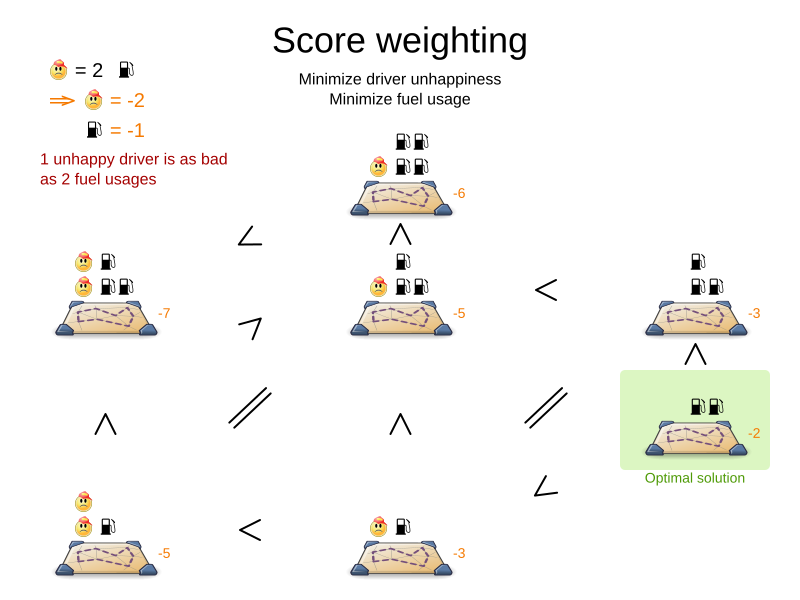
Score weighting is easy in use cases where you can put a price tag on everything. In that case, the positive constraints maximize revenue and the negative constraints minimize expenses, so together they maximize profit. Alternatively, score weighting is also often used to create social fairness. For example, a nurse, who requests a free day, pays a higher weight on New Years eve than on a normal day.
The weight of a constraint match can depend on the planning entities involved.
For example in cloud balancing, the weight of the soft constraint match for an active Computer
is the maintenance cost of that Computer (which differs per computer).
Putting a good weight on a constraint is often a difficult analytical decision, because it is about making choices and trade-offs against other constraints. Different stakeholders have different priorities. Don’t waste time with constraint weight discussions at the start of an implementation, instead add a constraint configuration and allow users to change them through a UI. A non-accurate weight is less damaging than mediocre algorithms:
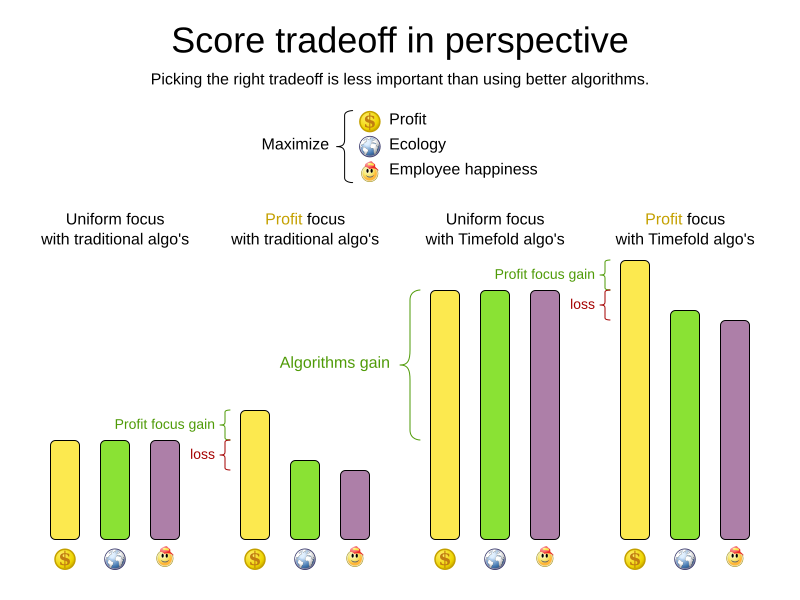
Most use cases use a Score with int weights, such as HardSoftScore.
1.5. Score constraint level (hard, soft, …)
Sometimes a score constraint outranks another score constraint, no matter how many times the latter is broken. In that case, those score constraints are in different levels. For example, a nurse cannot do two shifts at the same time (due to the constraints of physical reality), so this outranks all nurse happiness constraints.
Most use cases have only two score levels, hard and soft.
The levels of two scores are compared lexicographically.
The first score level gets compared first.
If those differ, the remaining score levels are ignored.
For example, a score that breaks 0 hard constraints and 1000000 soft constraints is better
than a score that breaks 1 hard constraint and 0 soft constraints.
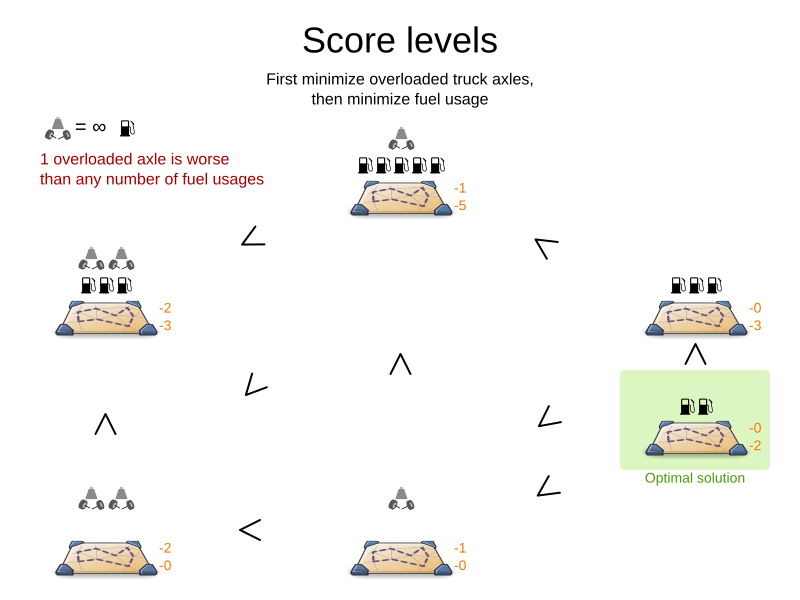
If there are two (or more) score levels, for example HardSoftScore, then a score is feasible if no hard constraints are broken.
|
By default, Timefold will always assign all planning variables a planning value. If there is no feasible solution, this means the best solution will be infeasible. To instead leave some of the planning entities unassigned, apply overconstrained planning. |
For each constraint, you need to pick a score level, a score weight and a score signum.
For example: -1soft which has score level of soft, a weight of 1 and a negative signum.
Do not use a big constraint weight when your business actually wants different score levels.
That hack, known as score folding, is broken:
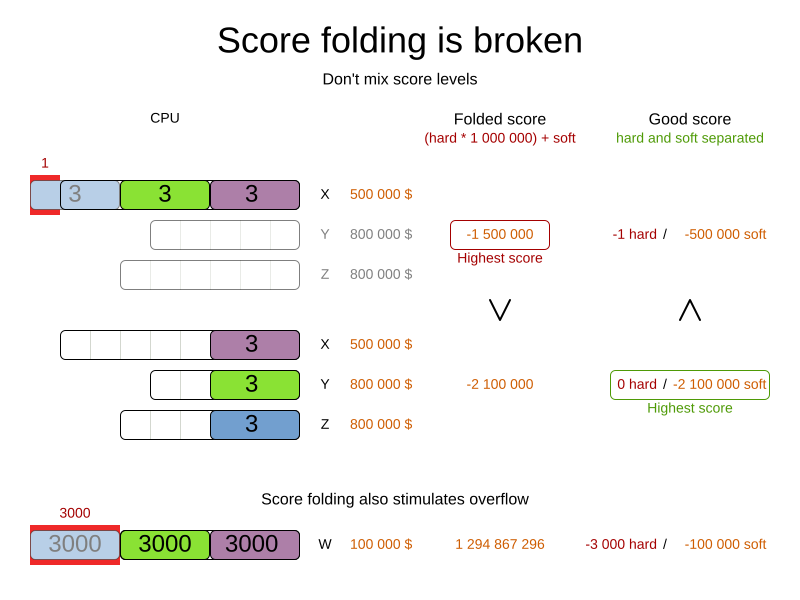
|
Your business might tell you that your hard constraints all have the same weight, because they cannot be broken (so the weight does not matter). This is not true because if no feasible solution exists for a specific dataset, the least infeasible solution allows the business to estimate how many business resources they are lacking. For example in cloud balancing, how many new computers to buy. Furthermore, it will likely create a score trap.
For example in cloud balance if a |
Three or more score levels are also supported. For example: a company might decide that profit outranks employee satisfaction (or vice versa), while both are outranked by the constraints of physical reality.
|
To model fairness or load balancing, there is no need to use lots of score levels (even though Timefold can handle many score levels). |
Most use cases use a Score with two or three weights,
such as HardSoftScore and HardMediumSoftScore.
1.6. Pareto scoring (AKA multi-objective optimization scoring)
Far less common is the use case of pareto optimization, which is also known as multi-objective optimization. In pareto scoring, score constraints are in the same score level, yet they are not weighted against each other. When two scores are compared, each of the score constraints are compared individually and the score with the most dominating score constraints wins. Pareto scoring can even be combined with score levels and score constraint weighting.
Consider this example with positive constraints, where we want to get the most apples and oranges. Since it is impossible to compare apples and oranges, we cannot weigh them against each other. Yet, despite that we cannot compare them, we can state that two apples are better than one apple. Similarly, we can state that two apples and one orange are better than just one orange. So despite our inability to compare some Scores conclusively (at which point we declare them equal), we can find a set of optimal scores. Those are called pareto optimal.
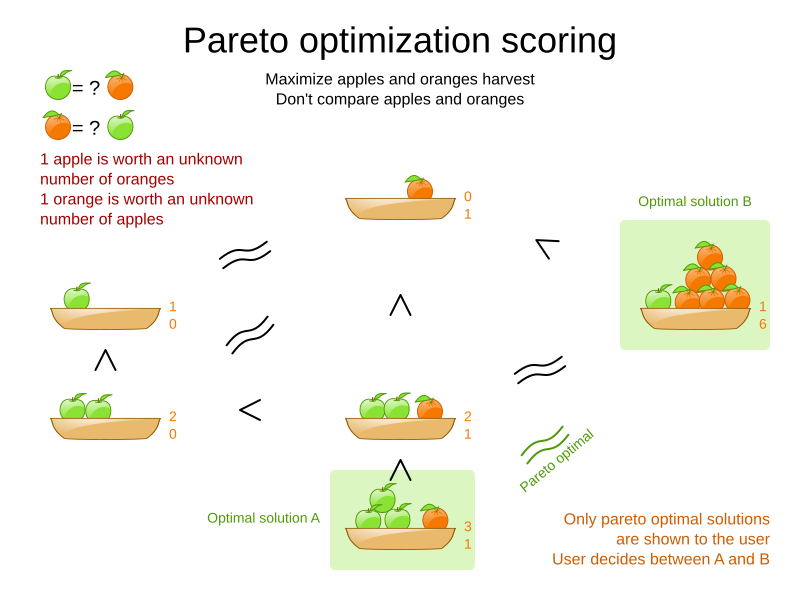
Scores are considered equal far more often. It is left up to a human to choose the better out of a set of best solutions (with equal scores) found by Timefold. In the example above, the user must choose between solution A (three apples and one orange) and solution B (one apple and six oranges). It is guaranteed that Timefold has not found another solution which has more apples or more oranges or even a better combination of both (such as two apples and three oranges).
Pareto scoring is currently not supported in Timefold.
|
A pareto |
1.7. Combining score techniques
All the score techniques mentioned above, can be combined seamlessly:
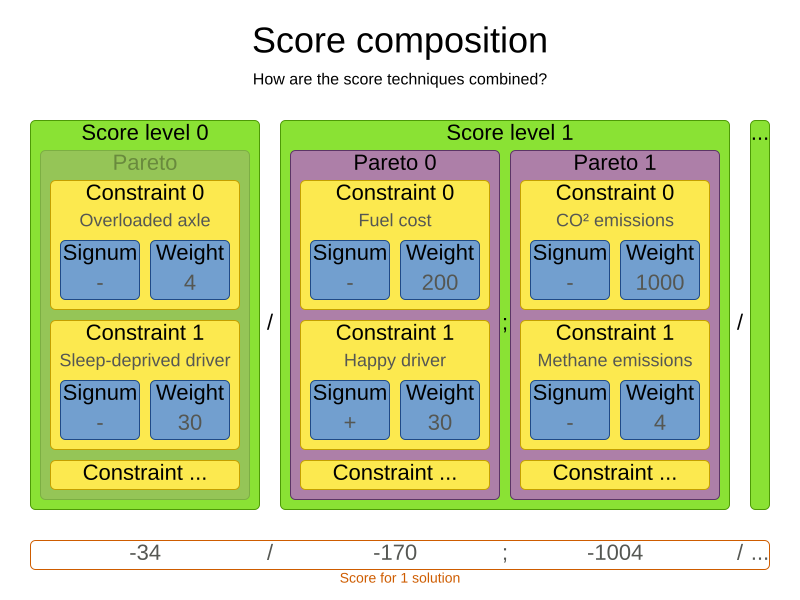
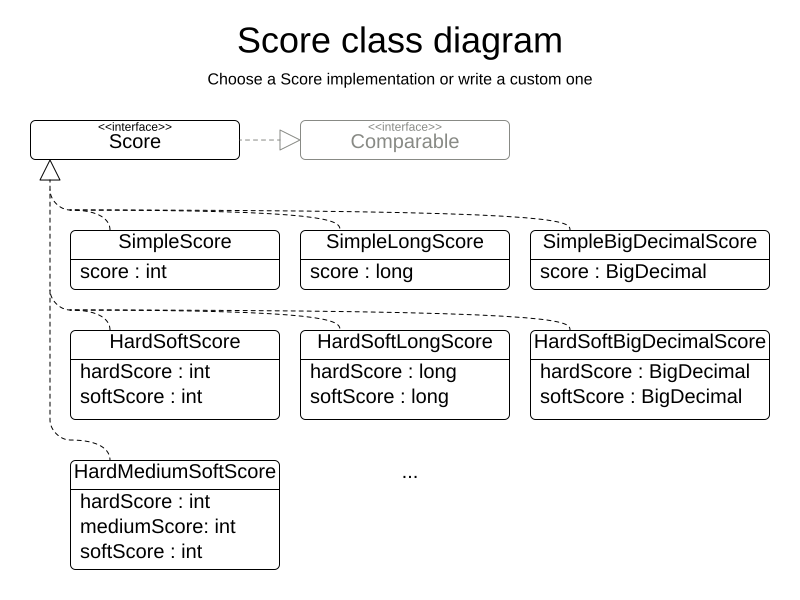
1.8. Score interface
A score is represented by the Score interface, which naturally extends Comparable:
public interface Score<...> extends Comparable<...> {
...
}The Score implementation to use depends on your use case.
Your score might not efficiently fit in a single long value.
Timefold has several built-in Score implementations, but you can implement a custom Score too.
Most use cases tend to use the built-in HardSoftScore.
All Score implementations also have an initScore (which is an int).It is mostly intended for internal use in Timefold: it is the negative number of uninitialized planning variables.
From a user’s perspective this is 0, unless a Construction Heuristic is terminated before it could initialize all planning variables (in which case Score.isSolutionInitialized() returns false).
The Score implementation (for example HardSoftScore) must be the same throughout a Solver runtime.
The Score implementation is configured in the solution domain class:
@PlanningSolution
public class CloudBalance {
...
@PlanningScore
private HardSoftScore score;
}1.9. Avoid floating point numbers in score calculation
Avoid the use of float or double in score calculation.
Use BigDecimal or scaled long instead.
Floating point numbers (float and double) cannot represent a decimal number correctly.
For example: a double cannot hold the value 0.05 correctly.
Instead, it holds the nearest representable value.
Arithmetic (including addition and subtraction) with floating point numbers, especially for planning problems, leads to incorrect decisions:
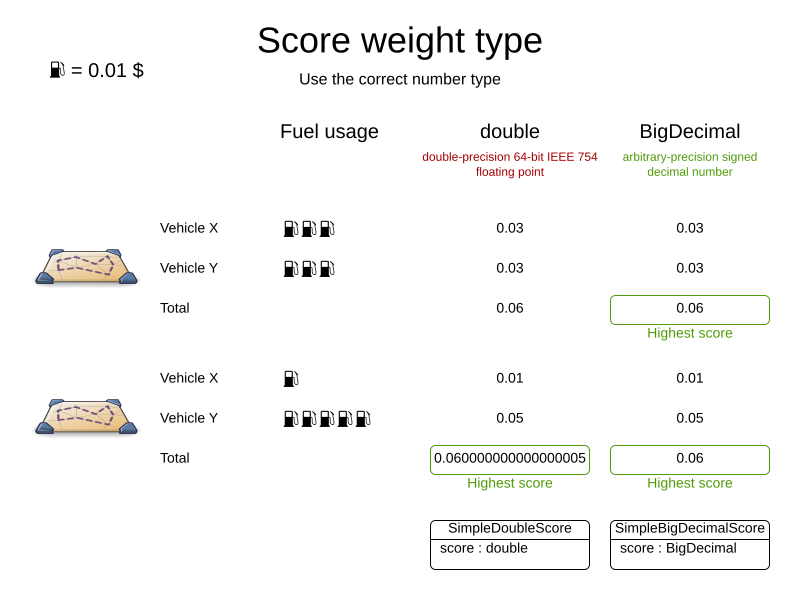
Additionally, floating point number addition is not associative:
System.out.println( ((0.01 + 0.02) + 0.03) == (0.01 + (0.02 + 0.03)) ); // returns falseThis leads to score corruption.
Decimal numbers (BigDecimal) have none of these problems.
|
BigDecimal arithmetic is considerably slower than Therefore, in many cases, it can be worthwhile to multiply all numbers for a single score weight by a plural of ten, so the score weight fits in a scaled |
2. Choose a score type
Depending on the number of score levels and type of score weights you need, choose a Score type.
Most use cases use a HardSoftScore.
|
To properly write a |
2.1. SimpleScore
A SimpleScore has a single int value, for example -123.
It has a single score level.
@PlanningScore
private SimpleScore score;Variants of this Score type:
-
SimpleLongScoreuses alongvalue instead of anintvalue. -
SimpleBigDecimalScoreuses aBigDecimalvalue instead of anintvalue.
2.2. HardSoftScore (Recommended)
A HardSoftScore has a hard int value and a soft int value, for example -123hard/-456soft.
It has two score levels (hard and soft).
@PlanningScore
private HardSoftScore score;Variants of this Score type:
-
HardSoftLongScoreuseslongvalues instead ofintvalues. -
HardSoftBigDecimalScoreusesBigDecimalvalues instead ofintvalues.
2.3. HardMediumSoftScore
A HardMediumSoftScore which has a hard int value, a medium int value and a soft int value, for example -123hard/-456medium/-789soft.
It has three score levels (hard, medium and soft).
The hard level determines if the solution is feasible,
and the medium level and soft level score values determine
how well the solution meets business goals.
Higher medium values take precedence over soft values irrespective of the soft value.
@PlanningScore
private HardMediumSoftScore score;Variants of this Score type:
-
HardMediumSoftLongScoreuseslongvalues instead ofintvalues. -
HardMediumSoftBigDecimalScoreusesBigDecimalvalues instead ofintvalues.
2.4. BendableScore
A BendableScore has a configurable number of score levels.
It has an array of hard int values and an array of soft int values,
for example with two hard levels and three soft levels, the score can be [-123/-456]hard/[-789/-012/-345]soft.
In that case, it has five score levels.
A solution is feasible if all hard levels are at least zero.
A BendableScore with one hard level and one soft level is equivalent to a HardSoftScore, while a BendableScore with one hard level and two soft levels is equivalent to a HardMediumSoftScore.
@PlanningScore(bendableHardLevelsSize = 2, bendableSoftLevelsSize = 3)
private BendableScore score;The number of hard and soft score levels need to be set at compilation time. It is not flexible to change during solving.
|
Do not use a Usually, multiple constraints share the same level and are weighted against each other. Use explaining the score to get the weight of individual constraints in the same level. |
Variants of this Score type:
-
BendableLongScoreuseslongvalues instead ofintvalues. -
BendableBigDecimalScoreusesBigDecimalvalues instead ofintvalues.
3. Calculate the Score
3.1. Score calculation types
There are several ways to calculate the Score of a solution:
-
Easy Java score calculation: Implement all constraints together in a single method in Java (or another JVM language). Does not scale.
-
Constraint streams score calculation: Implement each constraint as a separate Constraint Stream in Java (or another JVM language). Fast and scalable.
-
Incremental Java score calculation (not recommended): Implement multiple low-level methods in Java (or another JVM language). Fast and scalable. Very difficult to implement and maintain.
Every score calculation type can work with any Score definition (such as HardSoftScore or HardMediumSoftScore).
All score calculation types are Object Oriented and can reuse existing Java code.
|
The score calculation must be read-only. It must not change the planning entities or the problem facts in any way. For example, it must not call a setter method on a planning entity in the score calculation. Timefold does not recalculate the score of a solution if it can predict it (unless an environmentMode assertion is enabled). For example, after a winning step is done, there is no need to calculate the score because that move was done and undone earlier. As a result, there is no guarantee that changes applied during score calculation actually happen. To update planning entities when the planning variable change, use shadow variables instead. |
3.2. Easy Java score calculation
An easy way to implement your score calculation in Java.
-
Advantages:
-
Plain old Java: no learning curve
-
Opportunity to delegate score calculation to an existing code base or legacy system
-
-
Disadvantages:
-
Slower
-
Does not scale because there is no incremental score calculation
-
Implement the one method of the interface EasyScoreCalculator:
public interface EasyScoreCalculator<Solution_, Score_ extends Score<Score_>> {
Score_ calculateScore(Solution_ solution);
}For example in n queens:
public class NQueensEasyScoreCalculator
implements EasyScoreCalculator<NQueens, SimpleScore> {
@Override
public SimpleScore calculateScore(NQueens nQueens) {
int n = nQueens.getN();
List<Queen> queenList = nQueens.getQueenList();
int score = 0;
for (int i = 0; i < n; i++) {
for (int j = i + 1; j < n; j++) {
Queen leftQueen = queenList.get(i);
Queen rightQueen = queenList.get(j);
if (leftQueen.getRow() != null && rightQueen.getRow() != null) {
if (leftQueen.getRowIndex() == rightQueen.getRowIndex()) {
score--;
}
if (leftQueen.getAscendingDiagonalIndex() == rightQueen.getAscendingDiagonalIndex()) {
score--;
}
if (leftQueen.getDescendingDiagonalIndex() == rightQueen.getDescendingDiagonalIndex()) {
score--;
}
}
}
}
return SimpleScore.valueOf(score);
}
}Configure it in the solver configuration:
<scoreDirectorFactory>
<easyScoreCalculatorClass>ai.timefold.solver.examples.nqueens.optional.score.NQueensEasyScoreCalculator</easyScoreCalculatorClass>
</scoreDirectorFactory>To configure values of an EasyScoreCalculator dynamically in the solver configuration
(so the Benchmarker can tweak those parameters),
add the easyScoreCalculatorCustomProperties element and use custom properties:
<scoreDirectorFactory>
<easyScoreCalculatorClass>...MyEasyScoreCalculator</easyScoreCalculatorClass>
<easyScoreCalculatorCustomProperties>
<property name="myCacheSize" value="1000" />
</easyScoreCalculatorCustomProperties>
</scoreDirectorFactory>3.3. Incremental Java score calculation
A way to implement your score calculation incrementally in Java.
-
Advantages:
-
Very fast and scalable
-
Currently the fastest if implemented correctly
-
-
-
Disadvantages:
-
Hard to write
-
A scalable implementation heavily uses maps, indexes, … (things ConstraintStreams does for you)
-
You have to learn, design, write and improve all these performance optimizations yourself
-
-
Hard to read
-
Regular score constraint changes can lead to a high maintenance cost
-
-
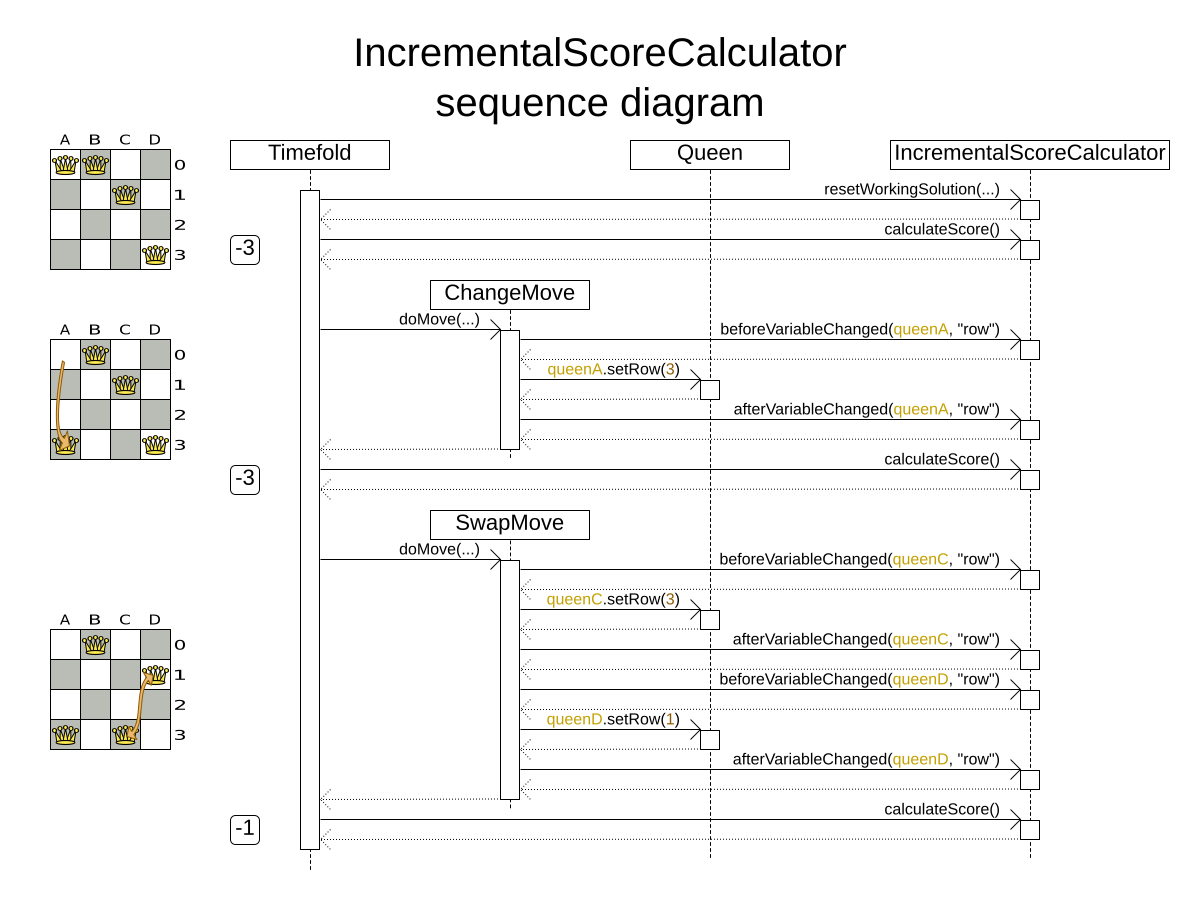
Implement all the methods of the interface IncrementalScoreCalculator:
public interface IncrementalScoreCalculator<Solution_, Score_ extends Score<Score_>> {
void resetWorkingSolution(Solution_ workingSolution);
void beforeEntityAdded(Object entity);
void afterEntityAdded(Object entity);
void beforeVariableChanged(Object entity, String variableName);
void afterVariableChanged(Object entity, String variableName);
void beforeEntityRemoved(Object entity);
void afterEntityRemoved(Object entity);
Score_ calculateScore();
}
For example in n queens:
public class NQueensAdvancedIncrementalScoreCalculator
implements IncrementalScoreCalculator<NQueens, SimpleScore> {
private Map<Integer, List<Queen>> rowIndexMap;
private Map<Integer, List<Queen>> ascendingDiagonalIndexMap;
private Map<Integer, List<Queen>> descendingDiagonalIndexMap;
private int score;
public void resetWorkingSolution(NQueens nQueens) {
int n = nQueens.getN();
rowIndexMap = new HashMap<Integer, List<Queen>>(n);
ascendingDiagonalIndexMap = new HashMap<Integer, List<Queen>>(n * 2);
descendingDiagonalIndexMap = new HashMap<Integer, List<Queen>>(n * 2);
for (int i = 0; i < n; i++) {
rowIndexMap.put(i, new ArrayList<Queen>(n));
ascendingDiagonalIndexMap.put(i, new ArrayList<Queen>(n));
descendingDiagonalIndexMap.put(i, new ArrayList<Queen>(n));
if (i != 0) {
ascendingDiagonalIndexMap.put(n - 1 + i, new ArrayList<Queen>(n));
descendingDiagonalIndexMap.put((-i), new ArrayList<Queen>(n));
}
}
score = 0;
for (Queen queen : nQueens.getQueenList()) {
insert(queen);
}
}
public void beforeEntityAdded(Object entity) {
// Do nothing
}
public void afterEntityAdded(Object entity) {
insert((Queen) entity);
}
public void beforeVariableChanged(Object entity, String variableName) {
retract((Queen) entity);
}
public void afterVariableChanged(Object entity, String variableName) {
insert((Queen) entity);
}
public void beforeEntityRemoved(Object entity) {
retract((Queen) entity);
}
public void afterEntityRemoved(Object entity) {
// Do nothing
}
private void insert(Queen queen) {
Row row = queen.getRow();
if (row != null) {
int rowIndex = queen.getRowIndex();
List<Queen> rowIndexList = rowIndexMap.get(rowIndex);
score -= rowIndexList.size();
rowIndexList.add(queen);
List<Queen> ascendingDiagonalIndexList = ascendingDiagonalIndexMap.get(queen.getAscendingDiagonalIndex());
score -= ascendingDiagonalIndexList.size();
ascendingDiagonalIndexList.add(queen);
List<Queen> descendingDiagonalIndexList = descendingDiagonalIndexMap.get(queen.getDescendingDiagonalIndex());
score -= descendingDiagonalIndexList.size();
descendingDiagonalIndexList.add(queen);
}
}
private void retract(Queen queen) {
Row row = queen.getRow();
if (row != null) {
List<Queen> rowIndexList = rowIndexMap.get(queen.getRowIndex());
rowIndexList.remove(queen);
score += rowIndexList.size();
List<Queen> ascendingDiagonalIndexList = ascendingDiagonalIndexMap.get(queen.getAscendingDiagonalIndex());
ascendingDiagonalIndexList.remove(queen);
score += ascendingDiagonalIndexList.size();
List<Queen> descendingDiagonalIndexList = descendingDiagonalIndexMap.get(queen.getDescendingDiagonalIndex());
descendingDiagonalIndexList.remove(queen);
score += descendingDiagonalIndexList.size();
}
}
public SimpleScore calculateScore() {
return SimpleScore.valueOf(score);
}
}Configure it in the solver configuration:
<scoreDirectorFactory>
<incrementalScoreCalculatorClass>ai.timefold.solver.examples.nqueens.optional.score.NQueensAdvancedIncrementalScoreCalculator</incrementalScoreCalculatorClass>
</scoreDirectorFactory>|
A piece of incremental score calculator code can be difficult to write and to review.
Assert its correctness by using an |
To configure values of an IncrementalScoreCalculator dynamically in the solver configuration
(so the Benchmarker can tweak those parameters),
add the incrementalScoreCalculatorCustomProperties element and use custom properties:
<scoreDirectorFactory>
<incrementalScoreCalculatorClass>...MyIncrementalScoreCalculator</incrementalScoreCalculatorClass>
<incrementalScoreCalculatorCustomProperties>
<property name="myCacheSize" value="1000"/>
</incrementalScoreCalculatorCustomProperties>
</scoreDirectorFactory>3.3.1. ConstraintMatchAwareIncrementalScoreCalculator
Optionally, also implement the ConstraintMatchAwareIncrementalScoreCalculator interface to:
-
Explain a score by splitting it up per score constraint with
ScoreExplanation.getConstraintMatchTotalMap(). -
Visualize or sort planning entities by how many constraints each one breaks with
ScoreExplanation.getIndictmentMap(). -
Receive a detailed analysis if the
IncrementalScoreCalculatoris corrupted inFAST_ASSERTorFULL_ASSERTenvironmentMode,
public interface ConstraintMatchAwareIncrementalScoreCalculator<Solution_, Score_ extends Score<Score_>> {
void resetWorkingSolution(Solution_ workingSolution, boolean constraintMatchEnabled);
Collection<ConstraintMatchTotal<Score_>> getConstraintMatchTotals();
Map<Object, Indictment<Score_>> getIndictmentMap();
}For example in machine reassignment, create one ConstraintMatchTotal per constraint type and call addConstraintMatch() for each constraint match:
public class MachineReassignmentIncrementalScoreCalculator
implements ConstraintMatchAwareIncrementalScoreCalculator<MachineReassignment, HardSoftLongScore> {
...
@Override
public void resetWorkingSolution(MachineReassignment workingSolution, boolean constraintMatchEnabled) {
resetWorkingSolution(workingSolution);
// ignore constraintMatchEnabled, it is always presumed enabled
}
@Override
public Collection<ConstraintMatchTotal<HardSoftLongScore>> getConstraintMatchTotals() {
ConstraintMatchTotal<HardSoftLongScore> maximumCapacityMatchTotal = new DefaultConstraintMatchTotal<>(CONSTRAINT_PACKAGE,
"maximumCapacity", HardSoftLongScore.ZERO);
...
for (MrMachineScorePart machineScorePart : machineScorePartMap.values()) {
for (MrMachineCapacityScorePart machineCapacityScorePart : machineScorePart.machineCapacityScorePartList) {
if (machineCapacityScorePart.maximumAvailable < 0L) {
maximumCapacityMatchTotal.addConstraintMatch(
Arrays.asList(machineCapacityScorePart.machineCapacity),
HardSoftLongScore.valueOf(machineCapacityScorePart.maximumAvailable, 0));
}
}
}
...
List<ConstraintMatchTotal<HardSoftLongScore>> constraintMatchTotalList = new ArrayList<>(4);
constraintMatchTotalList.add(maximumCapacityMatchTotal);
...
return constraintMatchTotalList;
}
@Override
public Map<Object, Indictment<HardSoftLongScore>> getIndictmentMap() {
return null; // Calculate it non-incrementally from getConstraintMatchTotals()
}
}That getConstraintMatchTotals() code often duplicates some of the logic of the normal IncrementalScoreCalculator methods.
Constraint Streams doesn’t have this disadvantage, because they are constraint match aware automatically when needed,
without any extra domain-specific code.
3.4. InitializingScoreTrend
The InitializingScoreTrend specifies how the Score will change as more and more variables are initialized (while the already initialized variables do not change). Some optimization algorithms (such Construction Heuristics and Exhaustive Search) run faster if they have such information.
For the Score (or each score level separately), specify a trend:
-
ANY(default): Initializing an extra variable can change the score positively or negatively. Gives no performance gain. -
ONLY_UP(rare): Initializing an extra variable can only change the score positively. Implies that:-
There are only positive constraints
-
And initializing the next variable cannot unmatch a positive constraint that was matched by a previous initialized variable.
-
-
ONLY_DOWN: Initializing an extra variable can only change the score negatively. Implies that:-
There are only negative constraints
-
And initializing the next variable cannot unmatch a negative constraint that was matched by a previous initialized variable.
-
Most use cases only have negative constraints.
Many of those have an InitializingScoreTrend that only goes down:
<scoreDirectorFactory>
<constraintProviderClass>ai.timefold.solver.examples.cloudbalancing.score.CloudBalancingConstraintProvider</constraintProviderClass>
<initializingScoreTrend>ONLY_DOWN</initializingScoreTrend>
</scoreDirectorFactory>Alternatively, you can also specify the trend for each score level separately:
<scoreDirectorFactory>
<constraintProviderClass>ai.timefold.solver.examples.cloudbalancing.score.CloudBalancingConstraintProvider</constraintProviderClass>
<initializingScoreTrend>ONLY_DOWN/ONLY_DOWN</initializingScoreTrend>
</scoreDirectorFactory>3.5. Invalid score detection
When you put the environmentMode in FULL_ASSERT (or FAST_ASSERT),
it will detect score corruption in the incremental score calculation.
However, that will not verify that your score calculator actually implements your score constraints as your business desires.
For example, one constraint might consistently match the wrong pattern.
To verify the constraints against an independent implementation, configure a assertionScoreDirectorFactory:
<environmentMode>FAST_ASSERT</environmentMode>
...
<scoreDirectorFactory>
<constraintProviderClass>ai.timefold.solver.examples.nqueens.optional.score.NQueensConstraintProvider</constraintProviderClass>
<assertionScoreDirectorFactory>
<easyScoreCalculatorClass>ai.timefold.solver.examples.nqueens.optional.score.NQueensEasyScoreCalculator</easyScoreCalculatorClass>
</assertionScoreDirectorFactory>
</scoreDirectorFactory>This way, the NQueensConstraintProvider implementation is validated by the EasyScoreCalculator.
|
This works well to isolate score corruption, but to verify that the constraint implement the real business needs, a unit test with a ConstraintVerifier is usually better. |
4. Score calculation performance tricks
4.1. Overview
The Solver will normally spend most of its execution time running the score calculation
(which is called in its deepest loops).
Faster score calculation will return the same solution in less time with the same algorithm,
which normally means a better solution in equal time.
4.2. Score calculation speed
After solving a problem, the Solver will log the score calculation speed per second.
This is a good measurement of Score calculation performance,
despite that it is affected by non score calculation execution time.
It depends on the problem scale of the problem dataset.
Normally, even for high scale problems, it is higher than 1000, except if you are using an EasyScoreCalculator.
|
When improving your score calculation, focus on maximizing the score calculation speed, instead of maximizing the best score. A big improvement in score calculation can sometimes yield little or no best score improvement, for example when the algorithm is stuck in a local or global optima. If you are watching the calculation speed instead, score calculation improvements are far more visible. Furthermore, watching the calculation speed allows you to remove or add score constraints, and still compare it with the original’s calculation speed. Comparing the best score with the original’s best score is pointless: it’s comparing apples and oranges. |
4.3. Incremental score calculation (with deltas)
When a solution changes, incremental score calculation (AKA delta based score calculation)
calculates the delta with the previous state to find the new Score,
instead of recalculating the entire score on every solution evaluation.
For example, when a single queen A moves from row 1 to 2,
it will not bother to check if queen B and C can attack each other, since neither of them changed:
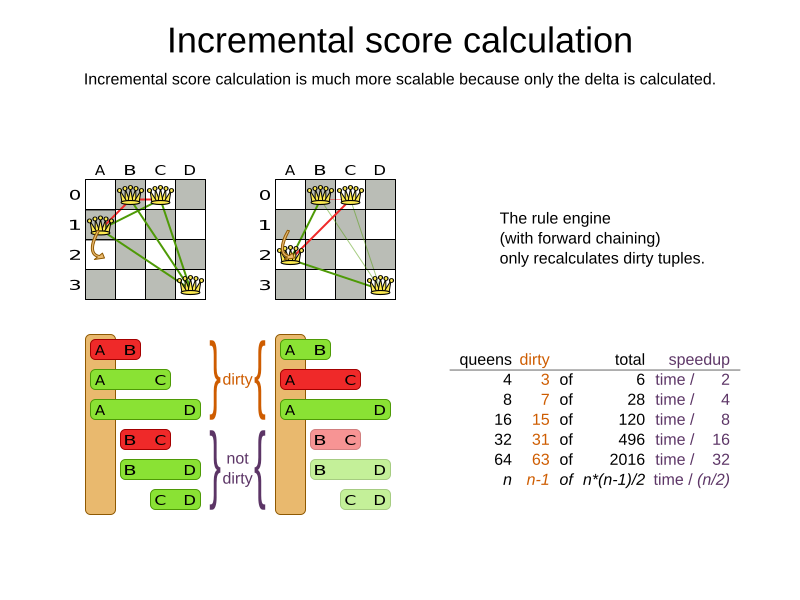
Similarly in employee rostering:
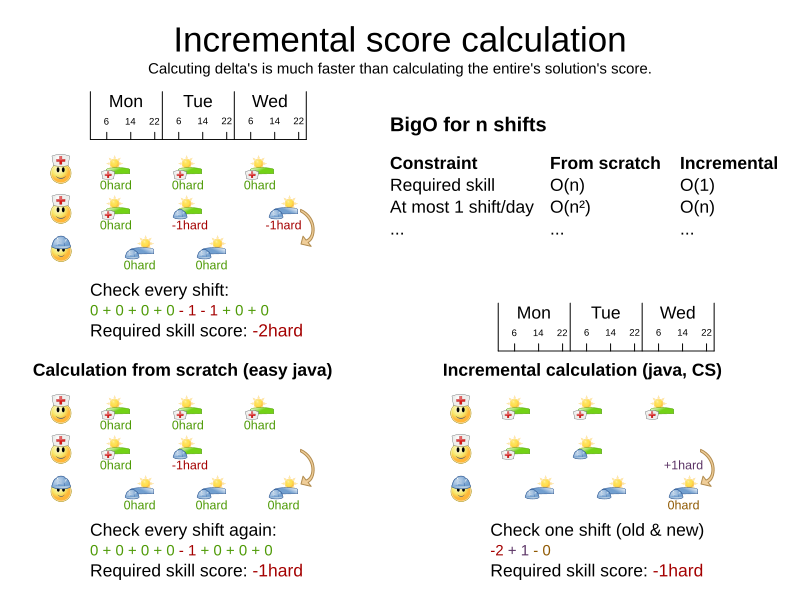
This is a huge performance and scalability gain. Constraint Streams gives you this huge scalability gain without forcing you to write a complicated incremental score calculation algorithm. Just let the rule engine do the hard work.
Notice that the speedup is relative to the size of your planning problem (your n), making incremental score calculation far more scalable.
4.4. Avoid calling remote services during score calculation
Do not call remote services in your score calculation (except if you are bridging EasyScoreCalculator to a legacy system). The network latency will kill your score calculation performance.
Cache the results of those remote services if possible.
If some parts of a constraint can be calculated once, when the Solver starts, and never change during solving,
then turn them into cached problem facts.
4.5. Pointless constraints
If you know a certain constraint can never be broken (or it is always broken), do not write a score constraint for it.
For example in n queens, the score calculation does not check if multiple queens occupy the same column,
because a Queen's column never changes and every solution starts with each Queen on a different column.
|
Do not go overboard with this. If some datasets do not use a specific constraint but others do, just return out of the constraint as soon as you can. There is no need to dynamically change your score calculation based on the dataset. |
4.6. Built-in hard constraint
Instead of implementing a hard constraint, it can sometimes be built in.
For example, if Lecture A should never be assigned to Room X, but it uses ValueRangeProvider on Solution,
so the Solver will often try to assign it to Room X too (only to find out that it breaks a hard constraint).
Use a ValueRangeProvider on the planning entity or filtered selection to define that Course A should only be assigned a Room different than X.
This can give a good performance gain in some use cases, not just because the score calculation is faster, but mainly because most optimization algorithms will spend less time evaluating infeasible solutions. However, usually this is not a good idea because there is a real risk of trading short term benefits for long term harm:
-
Many optimization algorithms rely on the freedom to break hard constraints when changing planning entities, to get out of local optima.
-
Both implementation approaches have limitations (feature compatibility, disabling automatic performance optimizations), as explained in their documentation.
4.7. Other score calculation performance tricks
-
Verify that your score calculation happens in the correct
Numbertype. If you are making the sum ofintvalues, do not sum it in adoublewhich takes longer. -
For optimal performance, always use server mode (
java -server). We have seen performance increases of 50% by turning on server mode. -
For optimal performance, use the latest Java version. For example, in the past we have seen performance increases of 30% by switching from java 1.5 to 1.6.
-
Always remember that premature optimization is the root of all evil. Make sure your design is flexible enough to allow configuration based tweaking.
4.8. Score trap
Make sure that none of your score constraints cause a score trap. A trapped score constraint uses the same weight for different constraint matches, when it could just as easily use a different weight. It effectively lumps its constraint matches together, which creates a flatlined score function for that constraint. This can cause a solution state in which several moves need to be done to resolve or lower the weight of that single constraint. Some examples of score traps:
-
You need two doctors at each table, but you are only moving one doctor at a time. So the solver has no incentive to move a doctor to a table with no doctors. Punish a table with no doctors more than a table with only one doctor in that score constraint in the score function.
-
Two exams need to be conducted at the same time, but you are only moving one exam at a time. So the solver has to move one of those exams to another timeslot without moving the other in the same move. Add a coarse-grained move that moves both exams at the same time.
For example, consider this score trap. If the blue item moves from an overloaded computer to an empty computer, the hard score should improve. The trapped score implementation fails to do that:
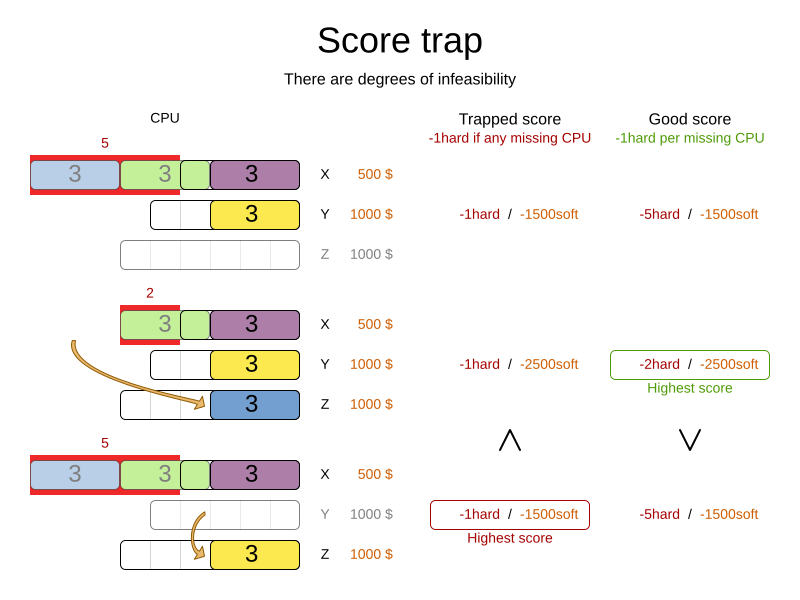
The Solver should eventually get out of this trap, but it will take a lot of effort (especially if there are even more processes on the overloaded computer). Before they do that, they might actually start moving more processes into that overloaded computer, as there is no penalty for doing so.
|
Avoiding score traps does not mean that your score function should be smart enough to avoid local optima. Leave it to the optimization algorithms to deal with the local optima. Avoiding score traps means to avoid, for each score constraint individually, a flatlined score function. |
|
Always specify the degree of infeasibility. The business will often say "if the solution is infeasible, it does not matter how infeasible it is." While that is true for the business, it is not true for score calculation as it benefits from knowing how infeasible it is. In practice, soft constraints usually do this naturally and it is just a matter of doing it for the hard constraints too. |
There are several ways to deal with a score trap:
-
Improve the score constraint to make a distinction in the score weight. For example, penalize
-1hardfor every missing CPU, instead of just-1hardif any CPU is missing. -
If changing the score constraint is not allowed from the business perspective, add a lower score level with a score constraint that makes such a distinction. For example, penalize
-1subsoftfor every missing CPU, on top of-1hardif any CPU is missing. The business ignores the subsoft score level. -
Add coarse-grained moves and union select them with the existing fine-grained moves. A coarse-grained move effectively does multiple moves to directly get out of a score trap with a single move. For example, move multiple items from the same container to another container.
4.9. stepLimit benchmark
Not all score constraints have the same performance cost. Sometimes one score constraint can kill the score calculation performance outright. Use the Benchmarker to do a one minute run and check what happens to the score calculation speed if you comment out all but one of the score constraints.
4.10. Fairness score constraints
Some use cases have a business requirement to provide a fair schedule (usually as a soft score constraint), for example:
-
Fairly distribute the workload amongst the employees, to avoid envy.
-
Evenly distribute the workload amongst assets, to improve reliability.
Implementing such a constraint can seem difficult (especially because there are different ways to formalize fairness), but usually the squared workload implementation behaves most desirable.
For each employee/asset, count the workload w and subtract w² from the score.
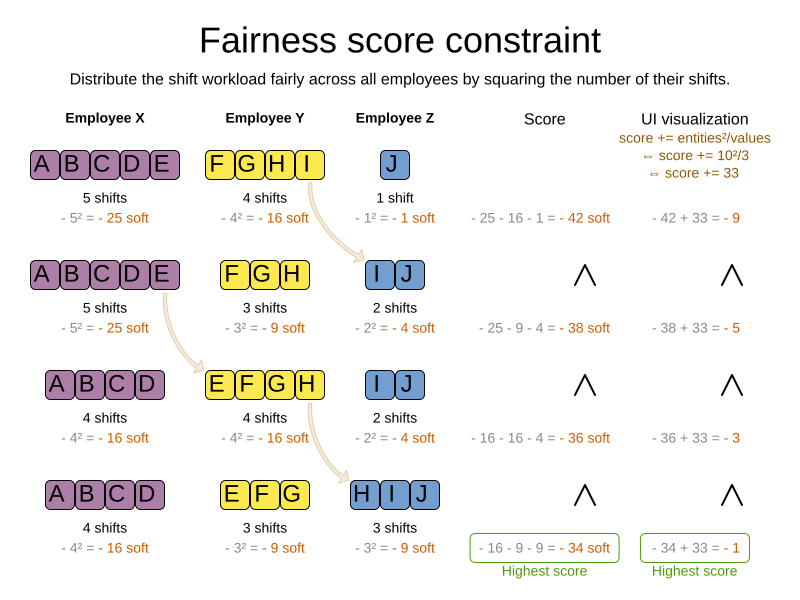
As shown above, the squared workload implementation guarantees that if you select two employees from a given solution and make their distribution between those two employees fairer, then the resulting new solution will have a better overall score. Do not just use the difference from the average workload, as that can lead to unfairness, as demonstrated below.
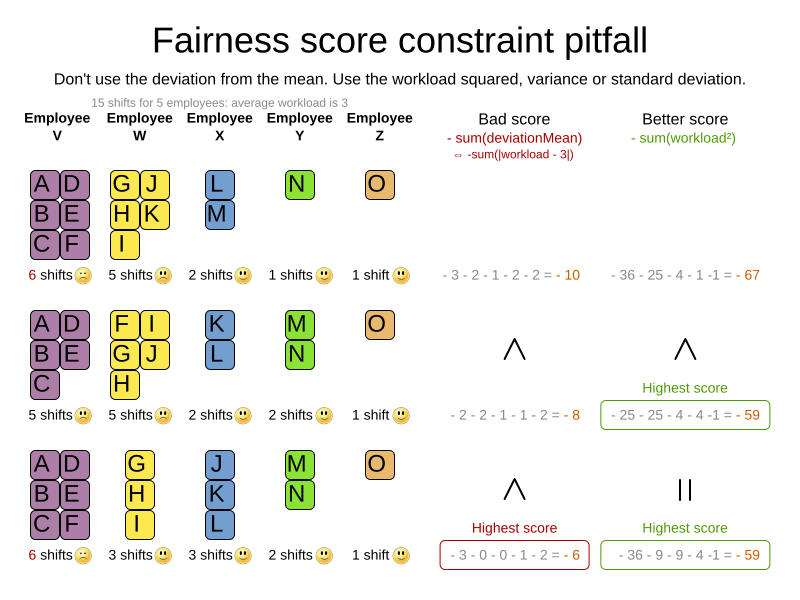
|
Instead of the squared workload, it is also possible to use the variance (squared difference to the average) or the standard deviation (square root of the variance). This has no effect on the score comparison, because the average will not change during planning. It is just more work to implement (because the average needs to be known) and trivially slower (because the calculation is a bit longer). |
When the workload is perfectly balanced, the user often likes to see a 0 score, instead of the distracting -34soft in the image above (for the last solution which is almost perfectly balanced).
To nullify this, either add the average multiplied by the number of entities to the score or instead show the variance or standard deviation in the UI.
5. Constraint configuration: adjust constraint weights dynamically
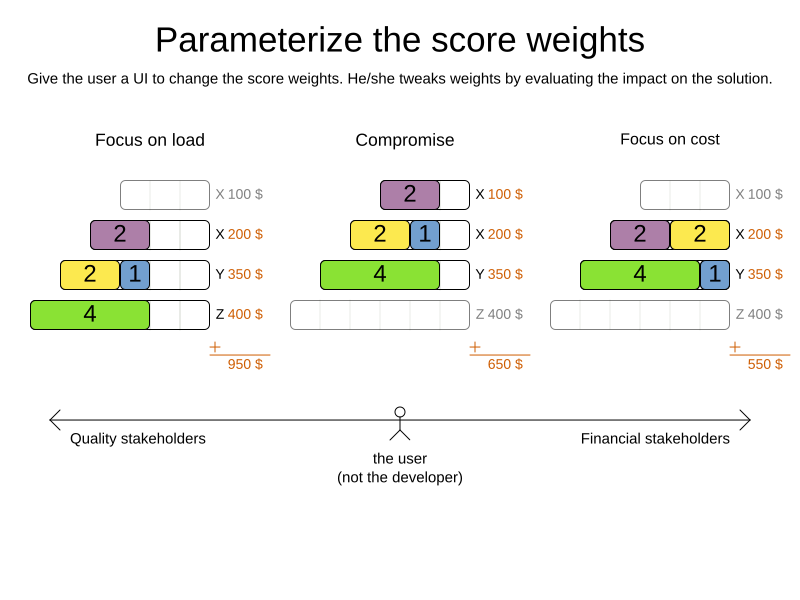
Deciding the correct weight and level for each constraint is not easy. It often involves negotiating with different stakeholders and their priorities. Furthermore, quantifying the impact of soft constraints is often a new experience for business managers, so they’ll need a number of iterations to get it right.
Don’t get stuck between a rock and a hard place. Provide a UI to adjust the constraint weights and visualize the resulting solution, so the business managers can tweak the constraint weights themselves:
5.1. Create a constraint configuration
First, create a new class to hold the constraint weights and other constraint parameters.
Annotate it with @ConstraintConfiguration:
@ConstraintConfiguration
public class ConferenceConstraintConfiguration {
...
}There will be exactly one instance of this class per planning solution.
The planning solution and the constraint configuration have a one-to-one relationship,
but they serve a different purpose, so they aren’t merged into a single class.
A @ConstraintConfiguration class can extend a parent @ConstraintConfiguration class,
which can be useful in international use cases with many regional constraints.
Add the constraint configuration on the planning solution
and annotate that field or property with @ConstraintConfigurationProvider:
@PlanningSolution
public class ConferenceSolution {
@ConstraintConfigurationProvider
private ConferenceConstraintConfiguration constraintConfiguration;
...
}The @ConstraintConfigurationProvider annotation automatically exposes the constraint configuration
as a problem fact, there is no need to add a @ProblemFactProperty annotation.
The constraint configuration class holds the constraint weights,
but it can also hold constraint parameters.
For example in conference scheduling, the minimum pause constraint has a constraint weight (like any other constraint),
but it also has a constraint parameter that defines the length of the minimum pause between two talks of the same speaker.
That pause length depends on the conference (= the planning problem):
in some big conferences 20 minutes isn’t enough to go from one room to the other.
That pause length is a field in the constraint configuration without a @ConstraintWeight annotation.
5.2. Add a constraint weight for each constraint
In the constraint configuration class, add a @ConstraintWeight field or property for each constraint:
@ConstraintConfiguration(constraintPackage = "...conferencescheduling.score")
public class ConferenceConstraintConfiguration {
@ConstraintWeight("Speaker conflict")
private HardMediumSoftScore speakerConflict = HardMediumSoftScore.ofHard(10);
@ConstraintWeight("Theme track conflict")
private HardMediumSoftScore themeTrackConflict = HardMediumSoftScore.ofSoft(10);
@ConstraintWeight("Content conflict")
private HardMediumSoftScore contentConflict = HardMediumSoftScore.ofSoft(100);
...
}The type of the constraint weights must be the same score class as the planning solution’s score member.
For example in conference scheduling, ConferenceSolution.getScore() and ConferenceConstraintConfiguration.getSpeakerConflict()
both return a HardMediumSoftScore.
A constraint weight cannot be null.
Give each constraint weight a default value, but expose them in a UI so the business users can tweak them.
The example above uses the ofHard(), ofMedium() and ofSoft() methods to do that.
Notice how it defaults the content conflict constraint as ten times more important than the theme track conflict constraint.
Normally, a constraint weight only uses one score level,
but it’s possible to use multiple score levels (at a small performance cost).
Each constraint has a constraint package and a constraint name, together they form the constraint id. These connect the constraint weight with the constraint implementation. For each constraint weight, there must be a constraint implementation with the same package and the same name.
-
The
@ConstraintConfigurationannotation has aconstraintPackageproperty that defaults to the package of the constraint configuration class. Cases with Constraint streams normally don’t need to specify it. -
The
@ConstraintWeightannotation has avaluewhich is the constraint name (for example "Speaker conflict"). It inherits the constraint package from the@ConstraintConfiguration, but it can override that, for example@ConstraintWeight(constraintPackage = "…region.france", …)to use a different constraint package than some other weights.
So every constraint weight ends up with a constraint package and a constraint name. Each constraint weight links with a constraint implementation, for example in Constraint Streams:
public final class ConferenceSchedulingConstraintProvider implements ConstraintProvider {
@Override
public Constraint[] defineConstraints(ConstraintFactory factory) {
return new Constraint[] {
speakerConflict(factory),
themeTrackConflict(factory),
contentConflict(factory),
...
};
}
protected Constraint speakerConflict(ConstraintFactory factory) {
return factory.forEachUniquePair(...)
...
.penalizeConfigurable("Speaker conflict", ...);
}
protected Constraint themeTrackConflict(ConstraintFactory factory) {
return factory.forEachUniquePair(...)
...
.penalizeConfigurable("Theme track conflict", ...);
}
protected Constraint contentConflict(ConstraintFactory factory) {
return factory.forEachUniquePair(...)
...
.penalizeConfigurable("Content conflict", ...);
}
...
}Each of the constraint weights defines the score level and score weight of their constraint.
The constraint implementation calls rewardConfigurable() or penalizeConfigurable() and the constraint weight is automatically applied.
If the constraint implementation provides a match weight, that match weight is multiplied with the constraint weight.
For example, the content conflict constraint weight defaults to 100soft
and the constraint implementation penalizes each match based on the number of shared content tags and the overlapping duration of the two talks:
@ConstraintWeight("Content conflict")
private HardMediumSoftScore contentConflict = HardMediumSoftScore.ofSoft(100);Constraint contentConflict(ConstraintFactory factory) {
return factory.forEachUniquePair(Talk.class,
overlapping(t -> t.getTimeslot().getStartDateTime(),
t -> t.getTimeslot().getEndDateTime()),
filtering((talk1, talk2) -> talk1.overlappingContentCount(talk2) > 0))
.penalizeConfigurable("Content conflict",
(talk1, talk2) -> talk1.overlappingContentCount(talk2)
* talk1.overlappingDurationInMinutes(talk2));
}So when 2 overlapping talks share only 1 content tag and overlap by 60 minutes, the score is impacted by -6000soft.
But when 2 overlapping talks share 3 content tags, the match weight is 180, so the score is impacted by -18000soft.
6. Explaining the score: which constraints are broken?
The easiest way to explain the score during development is to print the return value of getSummary(), but only use that method for diagnostic purposes:
System.out.println(scoreManager.getSummary(solution));For example in conference scheduling, this prints that talk S51 is responsible for breaking the hard constraint Speaker required room tag:
Explanation of score (-1hard/-806soft):
Constraint match totals:
-1hard: constraint (Speaker required room tag) has 1 matches:
-1hard: justifications ([S51])
-340soft: constraint (Theme track conflict) has 32 matches:
-20soft: justifications ([S68, S66])
-20soft: justifications ([S61, S44])
...
...
Indictments (top 5 of 72):
-1hard/-22soft: justification (S51) has 12 matches:
-1hard: constraint (Speaker required room tag)
-10soft: constraint (Theme track conflict)
...
...
|
Do not attempt to parse this string or use it in your UI or exposed services. Instead use the ConstraintMatch API below and do it properly. |
In the string above, there are two previously unexplained concepts.
Justifications are user-defined objects that implement the ai.timefold.solver.core.api.score.stream.ConstraintJustification interface,
which carry meaningful information about a constraint match, such as its package, name and score.
On the other hand, indicted objects are objects which were directly involved in causing a constraint to match. For example, if your constraints penalize each vehicle, then there will be one ai.timefold.solver.core.api.score.constraint.Indictment instance per vehicle, carrying the vehicle as an indicted object. Indictments are typically used for heat map visualization.
6.1. Using score calculation outside the Solver
If other parts of your application, for example your webUI, need to calculate the score of a solution, use the SolutionManager API:
SolutionManager<CloudBalance, HardSoftScore> scoreManager = SolutionManager.create(solverFactory);
ScoreExplanation<CloudBalance, HardSoftScore> scoreExplanation = scoreManager.explainScore(cloudBalance);Then use it when you need to calculate the Score of a solution:
HardSoftScore score = scoreExplanation.getScore();Furthermore, the ScoreExplanation can help explain the score through constraint match totals and/or indictments:
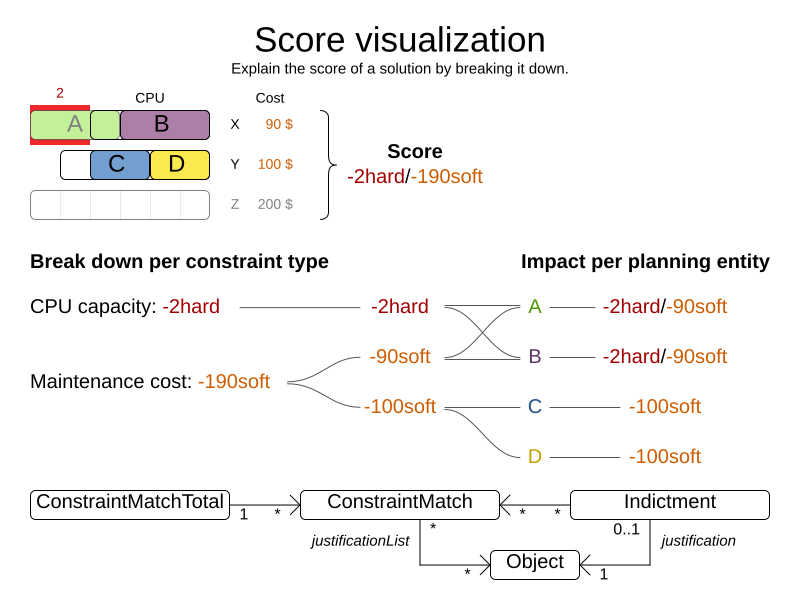
6.2. Break down the score by constraint justification
Each constraint may be justified by a different ConstraintJustification implementation, but you can also choose to share them among constraints.
To receive all constraint justifications regardless of their type, call:
List<ConstraintJustification> constraintJustificationlist = scoreExplanation.getJustificationList();
...In score DRL, justifications are always instances of
ai.timefold.solver.core.api.score.stream.DefaultConstraintJustification,
while in constraint streams, the return type can be customised,
so that it can be easily serialized and sent over the wire.
Such custom justifications can be queried like so:
List<MyConstraintJustification> constraintJustificationlist = scoreExplanation.getJustificationList(MyConstraintJustification.class);
...6.3. Break down the score by constraint
To break down the score per constraint, get the ConstraintMatchTotals from the ScoreExplanation:
Collection<ConstraintMatchTotal<HardSoftScore>> constraintMatchTotals = scoreExplanation.getConstraintMatchTotalMap().values();
for (ConstraintMatchTotal<HardSoftScore> constraintMatchTotal : constraintMatchTotals) {
String constraintName = constraintMatchTotal.getConstraintName();
// The score impact of that constraint
HardSoftScore totalScore = constraintMatchTotal.getScore();
for (ConstraintMatch<HardSoftScore> constraintMatch : constraintMatchTotal.getConstraintMatchSet()) {
ConstraintJustification justification = constraintMatch.getJustification();
HardSoftScore score = constraintMatch.getScore();
...
}
}Each ConstraintMatchTotal represents one constraint and has a part of the overall score.
The sum of all the ConstraintMatchTotal.getScore() equals the overall score.
|
Constraint streams supports constraint matches automatically, but incremental Java score calculation requires implementing an extra interface. |
6.4. Indictment heat map: visualize the hot planning entities
To show a heat map in the UI that highlights the planning entities and problem facts have an impact on the Score, get the Indictment map from the ScoreExplanation:
Map<Object, Indictment<HardSoftScore>> indictmentMap = scoreExplanation.getIndictmentMap();
for (CloudProcess process : cloudBalance.getProcessList()) {
Indictment<HardSoftScore> indictment = indictmentMap.get(process);
if (indictment == null) {
continue;
}
// The score impact of that planning entity
HardSoftScore totalScore = indictment.getScore();
for (ConstraintMatch<HardSoftScore> constraintMatch : indictment.getConstraintMatchSet()) {
String constraintName = constraintMatch.getConstraintName();
HardSoftScore score = constraintMatch.getScore();
...
}
}Each Indictment is the sum of all constraints where that justification object is involved with.
The sum of all the Indictment.getScoreTotal() differs from the overall score, because multiple Indictments can share the same ConstraintMatch.
|
Constraint streams supports constraint matches automatically, but incremental Java score calculation requires implementing an extra interface. |
7. Testing score constraints
It’s recommended to write a unit test for each score constraint individually to check that it behaves correctly. Different score calculation types come with different tools for testing. For more, see testing Constraint Streams.