Performance tips and tricks
Overview
The Solver will normally spend most of its execution time evaluating moves and running score calculation,
which is called in its deepest loops.
Faster score calculation will return the same solution in less time with the same algorithm,
which normally means a better solution in equal time.
Move evaluation and score calculation speed
After solving a problem, the Solver will log the move evaluation speed per second.
This is a good measurement of Move evaluation performance,
despite that it is affected by non-score calculation execution time.
It depends on the problem scale of the problem dataset.
Normally, even for large scale problems, it is higher than 1000,
except if you are using EasyScoreCalculator.
|
When improving your solver’s performance, focus on maximizing the score calculation speed while keeping the existing moves, instead of maximizing the best score. A big improvement in score calculation can sometimes yield little or no best score improvement, for example when the algorithm is stuck in a local or global optimum. If you are watching the calculation speed instead, score calculation improvements are far more visible. Furthermore, watching the calculation speed allows you to remove or add score constraints, and still compare it with the original’s calculation speed. Comparing the best score with the original’s best score is pointless: it’s comparing apples and oranges. |
The solver usually calculates the score for each move it evaluates.
This means a direct relationship exists between the score calculation and the evaluated move, typically a 1:1 ratio.
However, some moves,
such as Ruin and Recreate,
involve processing the score multiple times within the same move.
The use of moves like Ruin and Recreate may increase the number of score calculations,
making this ratio N:1.
Incremental score calculation (with deltas)
When a solution changes, incremental score calculation (AKA delta based score calculation)
calculates the delta with the previous state to find the new Score,
instead of recalculating the entire score on every solution evaluation.
For example, when a shift in employee rostering is reassigned from Ann to Beth, it will not bother to check any other employees, since neither of them changed:
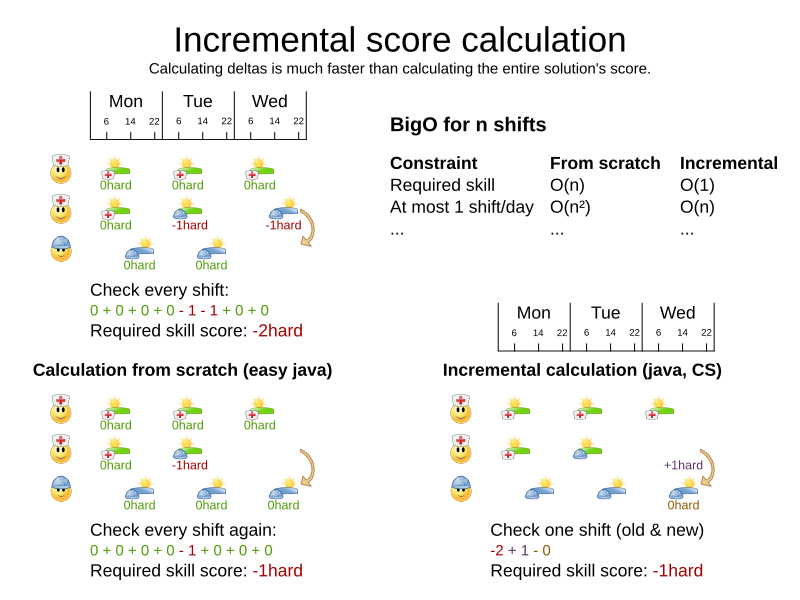
This is a huge performance and scalability gain. Constraint Streams API gives you this huge scalability gain without forcing you to write a complicated incremental score calculation algorithm.
Note that the speedup is relative to the size of your planning problem (your n), making incremental score calculation far more scalable.
Avoid calling remote services during score calculation
Do not call remote services in your score calculation,
except if you are bridging EasyScoreCalculator to a legacy system.
The network latency will kill your move evaluation performance.
Cache the results of those remote services if possible.
If some parts of a constraint can be calculated once, when the Solver starts, and never change during solving,
then turn them into cached problem facts.
Unused constraints
If a constraint is only relevant when certain data is present on the input (for example, if you want a capacity constraint to only be evaluated when capacity information is present), set the constraint weight to zero. In Constraint Streams, this will result in the constraint not being added to the node network and therefore have no performance impact at all.
Built-in hard constraint
Instead of implementing a hard constraint, it can sometimes be built in.
For example, if Lecture A should never be assigned to Room X, but it uses ValueRangeProvider on Solution,
so the Solver will often try to assign it to Room X too (only to find out that it breaks a hard constraint).
Use a ValueRangeProvider on the planning entity
or filtered selection
to define that Course A should only be assigned a Room different than X.
This can give a good performance gain in some use cases, not just because the move evaluation is faster, but mainly because most optimization algorithms will spend less time evaluating infeasible solutions. However, usually this is not a good idea because there is a real risk of trading short-term benefits for long-term harm:
-
Many optimization algorithms rely on the freedom to break hard constraints when changing planning entities, to get out of local optima.
-
Both implementation approaches have limitations (feature compatibility, disabling automatic performance optimizations), as explained in their documentation.
Large cross-products
In order for constraints to scale well, it is necessary to limit the amount of data that flows through them. In Constraint Streams, it starts with joins. Consider a school timetabling problem, where a teacher must not have two overlapping lessons. This is how the lesson could look:
-
Java
@PlanningEntity
class Lesson {
...
Teacher getTeacher() { ... }
boolean overlaps(Lesson anotherLesson) { ... }
boolean isCancelled() { ... }
...
}The simplest possible Constraint Stream we could write to penalize all overlapping lessons would then look like:
-
Java
constraintFactory.forEach(Lesson.class)
.join(Lesson.class)
.filter((leftLesson, rightLesson) ->
!leftLesson.isCancelled()
&& !rightLesson.isCancelled()
&& leftLesson.getTeacher()
.equals(rightLesson.getTeacher())
&& leftLesson.overlaps(rightLesson))
.penalize(HardSoftScore.ONE_HARD)
.asConstraint("Teacher lesson overlap")The join creates a cross-product between lessons, producing a match (also called a tuple) for every possible combination of two lessons, even though we know that many of these matches will not be penalized. This shows the problem in numbers:
| Number of lessons | Number of possible pairs |
|---|---|
10 |
100 |
100 |
10 000 |
1 000 |
1 000 000 |
To process a thousand lessons, the constraint first creates a cross-product of one million pairs, only to throw away pretty much all of them before penalizing. Reducing the size of the cross-product by half will therefore double the move evaluation speed.
Filters before joins
As the example shows, canceled lessons are eventually filtered out after the join. Let’s instead remove them from the cross-product entirely. For the first lesson in the join, also called “left,” we put the cancellation check before the join like so:
-
Java
constraintFactory.forEach(Lesson.class)
.filter(lesson -> !lesson.isCancelled())
.join(Lesson.class)
.filter((leftLesson, rightLesson) ->
!rightLesson.isCancelled()
&& leftLesson.getTeacher().equals(rightLesson.getTeacher())
&& leftLesson.overlaps(rightLesson))
...The canceled lessons are no longer coming in from the left, which reduces the cross-product. However, some canceled lessons are still coming in from the right through the join. They can be eliminated using a filtered nested stream:
-
Java
constraintFactory.forEach(Lesson.class)
.filter(lesson -> !lesson.isCancelled())
.join(
constraintFactory.forEach(Lesson.class)
.filter(lesson -> !lesson.isCancelled()))
.filter((leftLesson, rightLesson) ->
leftLesson.getTeacher().equals(rightLesson.getTeacher())
&& leftLesson.overlaps(rightLesson))
...We’ve created a new Constraint Stream from Lesson, filtering before it entered our join.
We have now applied the same improvement on both the left and right sides of the join,
making sure it only creates a cross-product of lessons which we care about.
Joiners over filters
Filters are just a simple check if a tuple matches a predicate.
If it does, it is propagated downstream, otherwise it is no longer evaluated.
Each tuple needs to go through this check, and that means every pair of lessons will be evaluated.
When a Lesson changes, all pairs with that Lesson will be wastefully re-evaluated.
Let’s move the Teacher equality check from the final filter above to a Joiner:
-
Java
constraintFactory.forEach(Lesson.class)
.filter(lesson -> !lesson.isCancelled())
.join(
constraintFactory.forEach(Lesson.class)
.filter(lesson -> !lesson.isCancelled()),
Joiners.equal(Lesson::getTeacher))
.filter(Lesson::overlaps)
...The constraint still says the same thing:
a Lesson pair will only be sent downstream if they share the same Teacher.
Unlike the filter, this brings the performance benefit of indexing.
Now when a Lesson changes, only the pairs with the matching Teacher will be re-evaluated.
So even though the cross-product remains the same, we are doing much less work processing it.
The final filter(Lesson::overlaps) now only performs one operation on the final cross product,
and the number of Lesson pairs that get this far is already reduced as much as possible.
Removing more and earlier
If at all possible, the Joiner that will remove more tuples than the others should be put first. The size of cross-products will be the same, but the processing will happen more quickly.
Consider a new situation, where lessons also have rooms in which they happen. Although there are possibly dozens of teachers, there are only three rooms. Therefore, the join should look like this:
-
Java
constraintFactory.forEach(Lesson.class)
.join(Lesson.class,
Joiners.equal(Lesson::getTeacher),
Joiners.equal(Lesson::getRoom))
...This way, we first create “buckets” for each of the many teachers, and these buckets will only contain a relatively small number of lessons per room. If done the other way around, there would be a small number of large buckets, leading to much more iteration every time a lesson changes.
For that reason, it is generally recommended putting Joiners based on enum fields or boolean fields last.
Indexing, Hashing, Looping
The code on the hot path of your application needs to be as fast as possible.
-
When you use Shadow Variables, you will provide a
suppliermethod that computes the value of the shadow variable. -
This method will be called very often during score calculation, so it needs to be fast.
-
If you need to do a lookup in a collection to find an element, ideally you are indexing into an array.
-
The second best option is to use a
HashMaporHashSet. -
Avoid using
java.util.Streamor any other form of explicit iteration in constraints, as that is much slower.
Enable automatic node sharing (Enterprise Edition only)
If you are using the Enterprise Edition, you should enable automatic node sharing as it can significantly speed up score calculation.
Benchmark
Whatever you do, benchmark on a large and diverse set of inputs.
JVM performance may differ by as much as 20% between runs. To decide whether your changes helped or made things worse, make sure to always average the move evaluation speed from multiple runs on the same machine with the same solver configuration. We provide a Benchmarker to help you with that.
Validate the implementation using FULL_ASSERT
When you are done optimizing your score calculation, make sure to validate it using FULL_ASSERT mode. Make sure not to run with this mode in production.
Other score calculation performance tricks
-
Verify that your score calculation happens in the correct
Numbertype. If you are making the sum ofintvalues, do not sum it in adoublewhich takes longer. -
For optimal performance, use the latest Java version. We often see significant performance improvements by switching to new Java versions.
-
Always remember that premature optimization is the root of all evil. Make sure your design is flexible enough to allow configuration-based tweaking.
Score trap
Make sure that none of your score constraints cause a score trap. A trapped score constraint uses the same weight for different constraint matches, when it could just as easily use a different weight. It effectively lumps its constraint matches together, which creates a flatlined score function for that constraint. This can cause a solution state in which several moves need to be done to resolve or lower the weight of that single constraint. Some examples of score traps:
-
You need two doctors at each table, but you are only moving one doctor at a time. So the solver has no incentive to move a doctor to a table with no doctors. Punish a table with no doctors more than a table with only one doctor in that score constraint in the score function.
-
Two exams need to be conducted at the same time, but you are only moving one exam at a time. So the solver has to move one of those exams to another timeslot without moving the other in the same move. Add a coarse-grained move that moves both exams at the same time.
For example, consider this score trap. If the blue process moves from an overloaded computer to an empty computer, the hard score should improve. The trapped score implementation fails to do that:
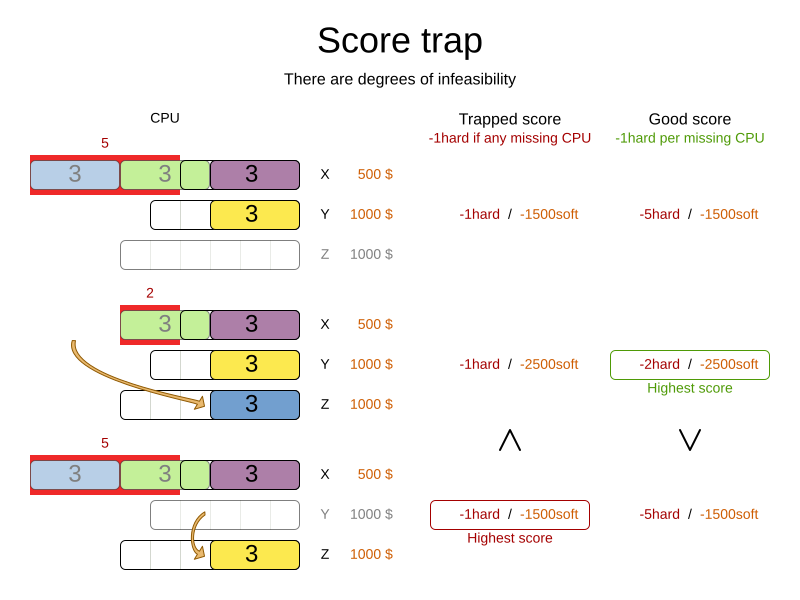
The Solver should eventually get out of this trap, but it will take a lot of effort (especially if there are even more processes on the overloaded computer). Before they do that, they might actually start moving more processes into that overloaded computer, as there is no penalty for doing so.
|
Avoiding score traps does not mean that your score function should be smart enough to avoid local optima. Leave it to the optimization algorithms to deal with the local optima. Avoiding score traps means to avoid, for each score constraint individually, a flatlined score function. |
|
Always specify the degree of infeasibility. The business will often say "if the solution is infeasible, it does not matter how infeasible it is." While that is true for the business, it is not true for score calculation as it benefits from knowing how infeasible it is. In practice, soft constraints usually do this naturally and it is just a matter of doing it for the hard constraints too. |
There are several ways to deal with a score trap:
-
Improve the score constraint to make a distinction in the score weight. For example, penalize
-1hardfor every missing CPU, instead of just-1hardif any CPU is missing. -
If changing the score constraint is not allowed from the business perspective, add a lower score level with a score constraint that makes such a distinction. For example, penalize
-1subsoftfor every missing CPU, on top of-1hardif any CPU is missing. The business ignores the subsoft score level. -
Add coarse-grained moves and union select them with the existing fine-grained moves. A coarse-grained move effectively does multiple moves to directly get out of a score trap with a single move. For example, move multiple items from the same container to another container.
stepLimit benchmark
Not all score constraints have the same performance cost. Sometimes one score constraint can ruin performance outright. Use the Benchmarker to do a one minute run and check what happens to the move evaluation speed if you comment out all but one of the score constraints.