Local search
1. Overview
Local Search starts from an initial solution and evolves that single solution into a mostly better and better solution. It uses a single search path of solutions, not a search tree. At each solution in this path it evaluates a number of moves on the solution and applies the most suitable move to take the step to the next solution. It does that for a high number of iterations until it’s terminated (usually because its time has run out).
Local Search acts a lot like a human planner: it uses a single search path and moves facts around to find a good feasible solution. Therefore it’s pretty natural to implement.
Local Search needs to start from an initialized solution, therefore it’s usually required to configure a Construction Heuristic phase before it.
2. Local search concepts
2.1. Step by step
A step is the winning Move.
Local Search tries a number of moves on the current solution and picks the best accepted move as the step:
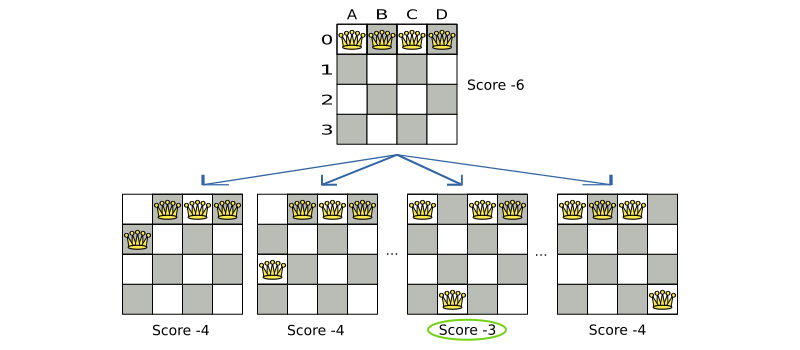
Because the move B0 to B3 has the highest score (-3), it is picked as the next step.
If multiple moves have the same highest score, one is picked randomly, in this case B0 to B3.
Note that C0 to C3 (not shown) could also have been picked because it also has the score -3.
The step is applied on the solution. From that new solution, Local Search tries every move again, to decide the next step after that. It continually does this in a loop, and we get something like this:
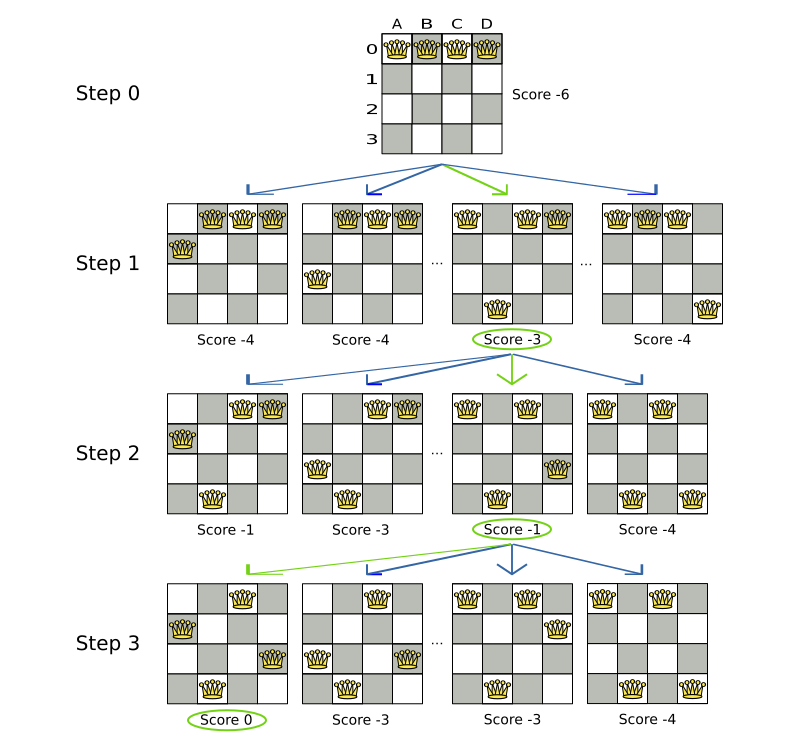
Notice that Local Search doesn’t use a search tree, but a search path. The search path is highlighted by the green arrows. At each step it tries all selected moves, but unless it’s the step, it doesn’t investigate that solution further. This is one of the reasons why Local Search is very scalable.
Local Search solves the four queens problem by starting with the starting solution and make the following steps sequentially:
-
B0 to B3
-
D0 to D2
-
A0 to A1
A naive Local Search configuration solves the four queens problem in three steps, by evaluating only 37 possible solutions (three steps with 12 moves each + one starting solution), which is only a fraction of all 256 possible solutions. It solves 16 queens in 31 steps, by evaluating only 7441 out of 18446744073709551616 possible solutions. By using a Construction Heuristics phase first, it’s even a lot more efficient.
2.2. Decide the next step
Local Search decides the next step with the aid of three configurable components:
-
A
MoveSelectorwhich selects the possible moves of the current solution. See move and neighborhood selection. -
An
Acceptorwhich filters out unacceptable moves. -
A
Foragerwhich gathers accepted moves and picks the next step from them.
The solver phase configuration looks like this:
<localSearch>
<unionMoveSelector>
...
</unionMoveSelector>
<acceptor>
...
</acceptor>
<forager>
...
</forager>
</localSearch>In the example below, the MoveSelector generated the moves shown with the blue lines,
the Acceptor accepted all of them and the Forager picked the move B0 to B3.

Turn on trace logging to show the decision making in the log.
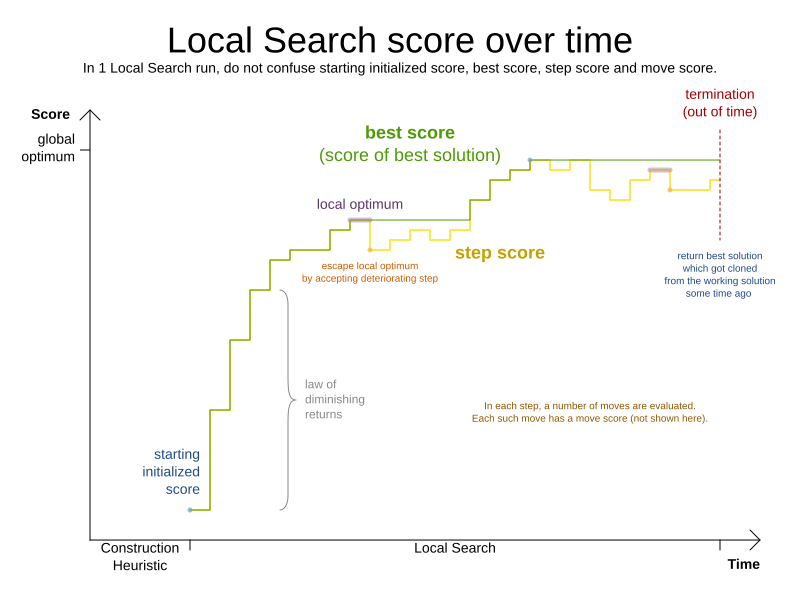
Because the last solution can degrade (such as in Tabu Search),
the Solver remembers the best solution it has encountered through the entire search path.
Each time the current solution is better than the last best solution,
the current solution is cloned
and referenced as the new best solution.
2.3. Acceptor
Use an Acceptor (together with a Forager) to activate Tabu Search, Simulated Annealing, Late Acceptance, … For each move it checks whether it is accepted or not.
By changing a few lines of configuration, you can easily switch from Tabu Search to Simulated Annealing or Late Acceptance and back.
You can implement your own Acceptor, but the built-in acceptors should suffice for most needs.
You can also combine multiple acceptors.
2.4. Forager
A Forager gathers all accepted moves and picks the move which is the next step.
Normally it picks the accepted move with the highest score.
If several accepted moves have the highest score, one is picked randomly to break the tie.
Breaking ties randomly leads to better results.
|
It is possible to disable breaking ties randomly by explicitly setting
|
2.4.1. Accepted count limit
When there are many possible moves, it becomes inefficient to evaluate all of them at every step. To evaluate only a random subset of all the moves, use:
-
An
acceptedCountLimitinteger, which specifies how many accepted moves should be evaluated during each step. By default, all accepted moves are evaluated at every step.<forager> <acceptedCountLimit>1000</acceptedCountLimit> </forager>
Unlike the N-queens problem, real world problems require the use of acceptedCountLimit.
Start from an acceptedCountLimit that takes a step in less than two seconds.
Turn on INFO logging to see the step times.
Use the Benchmarker to tweak the value.
|
With a low |
2.4.2. Pick early type
A forager can pick a move early during a step, ignoring subsequent selected moves. There are three pick early types for Local Search:
-
NEVER: A move is never picked early: all accepted moves are evaluated that the selection allows. This is the default.<forager> <pickEarlyType>NEVER</pickEarlyType> </forager> -
FIRST_BEST_SCORE_IMPROVING: Pick the first accepted move that improves the best score. If none improve the best score, it behaves exactly like the pickEarlyType NEVER.<forager> <pickEarlyType>FIRST_BEST_SCORE_IMPROVING</pickEarlyType> </forager> -
FIRST_LAST_STEP_SCORE_IMPROVING: Pick the first accepted move that improves the last step score. If none improve the last step score, it behaves exactly like the pickEarlyType NEVER.<forager> <pickEarlyType>FIRST_LAST_STEP_SCORE_IMPROVING</pickEarlyType> </forager>
3. Hill climbing (simple local search)
3.1. Algorithm description
Hill Climbing tries all selected moves and then takes the best move, which is the move which leads to the solution with the highest score. That best move is called the step move. From that new solution, it again tries all selected moves and takes the best move and continues like that iteratively. If multiple selected moves tie for the best move, one of them is randomly chosen as the best move.
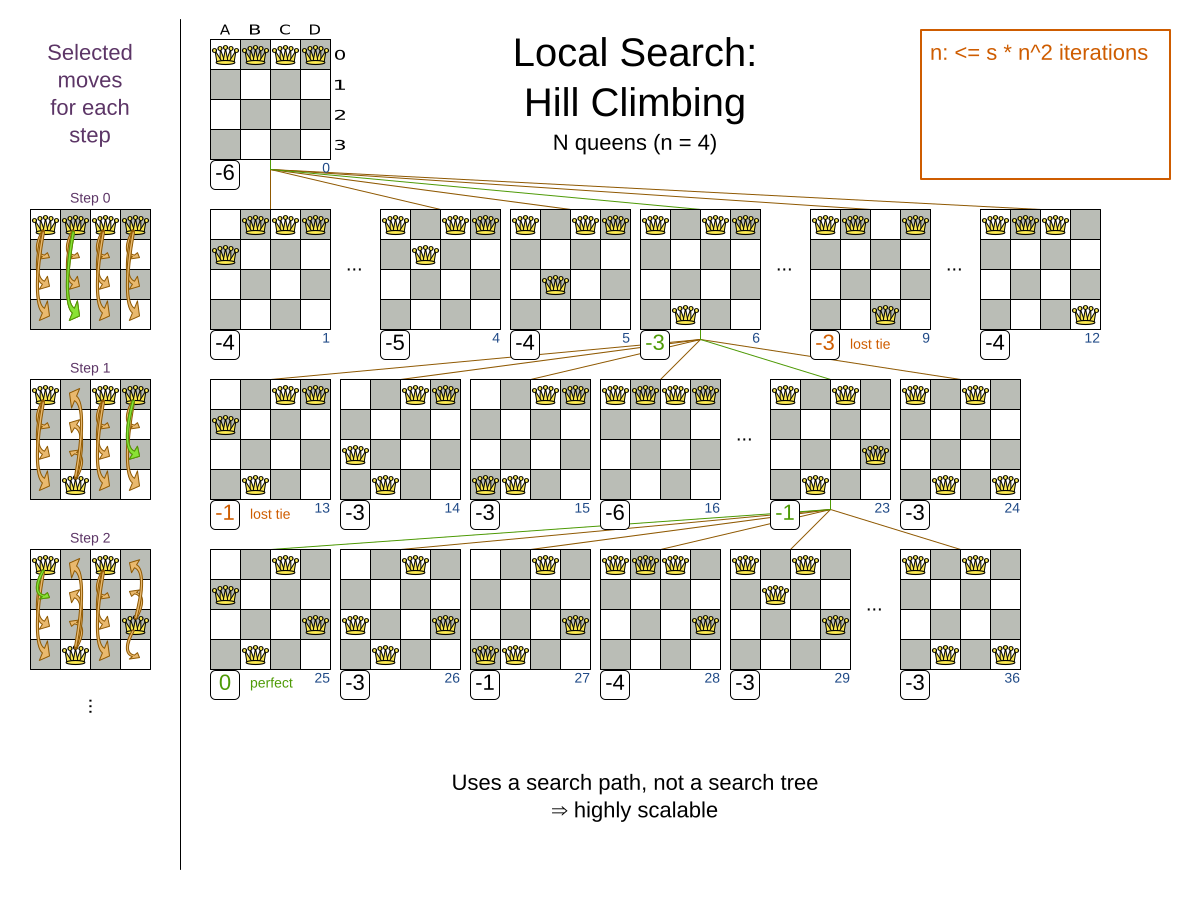
Notice that once a queen has moved, it can be moved again later. This is a good thing, because in an NP-complete problem it’s impossible to predict what will be the optimal final value for a planning variable.
3.2. Stuck in local optima
Hill climbing always takes improving moves. This may seem like a good thing, but it’s not: Hill Climbing can easily get stuck in a local optimum. This happens when it reaches a solution for which all the moves deteriorate the score. Even if it picks one of those moves, the next step might go back to the original solution and which case chasing its own tail:
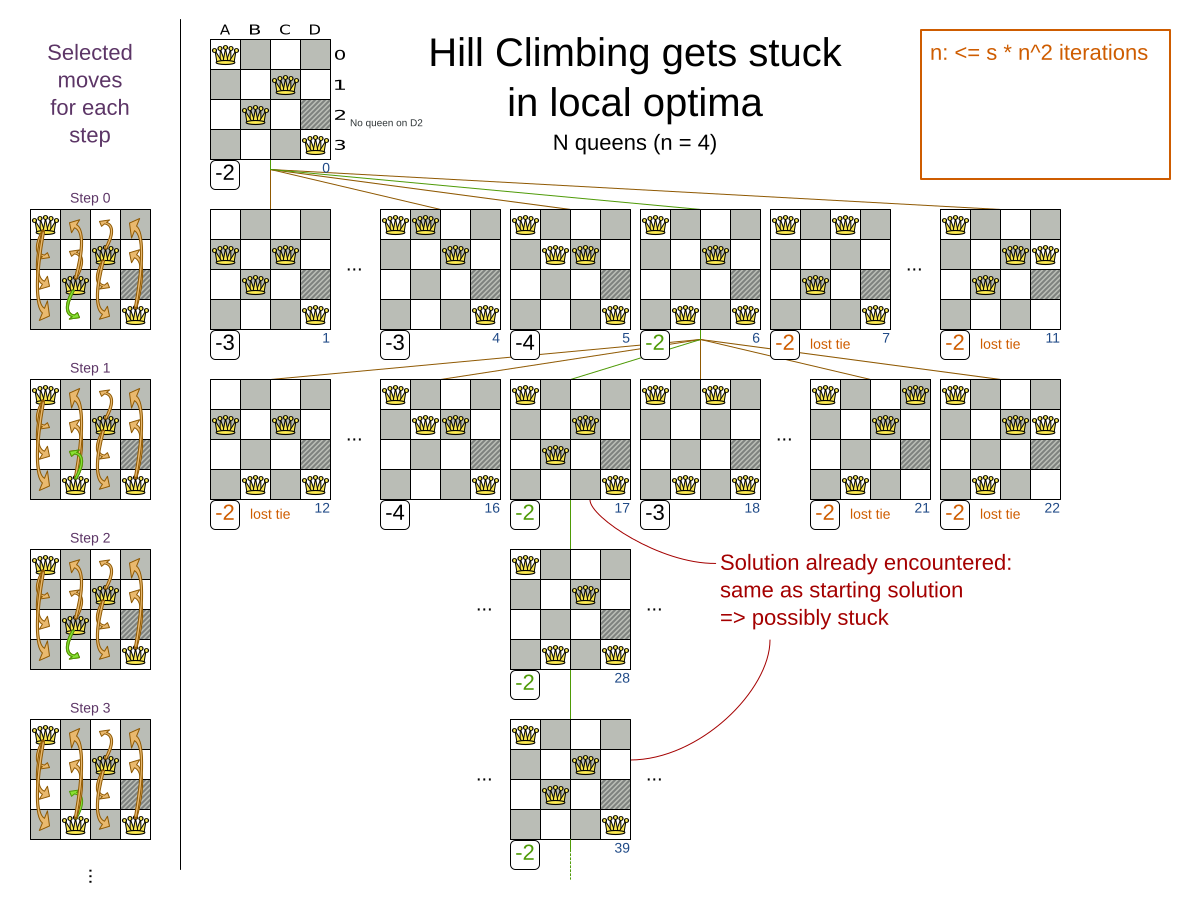
Improvements upon Hill Climbing (such as Tabu Search, Simulated Annealing and Late Acceptance) address the problem of being stuck in local optima. Therefore, it’s recommended to never use Hill Climbing, unless you’re absolutely sure there are no local optima in your planning problem.
3.3. Configuration
Simplest configuration:
<localSearch>
<localSearchType>HILL_CLIMBING</localSearchType>
</localSearch>Advanced configuration:
<localSearch>
...
<acceptor>
<acceptorType>HILL_CLIMBING</acceptorType>
</acceptor>
<forager>
<acceptedCountLimit>1</acceptedCountLimit>
</forager>
</localSearch>4. Tabu search
4.1. Algorithm description
Tabu Search is a Local Search that maintains a tabu list to avoid getting stuck in local optima. The tabu list holds recently used objects that are taboo to use for now. Moves that involve an object in the tabu list, are not accepted. The tabu list objects can be anything related to the move, such as the planning entity, planning value, move, solution, …
See example with entity tabu for four queens, so the queens are put in the tabu list:
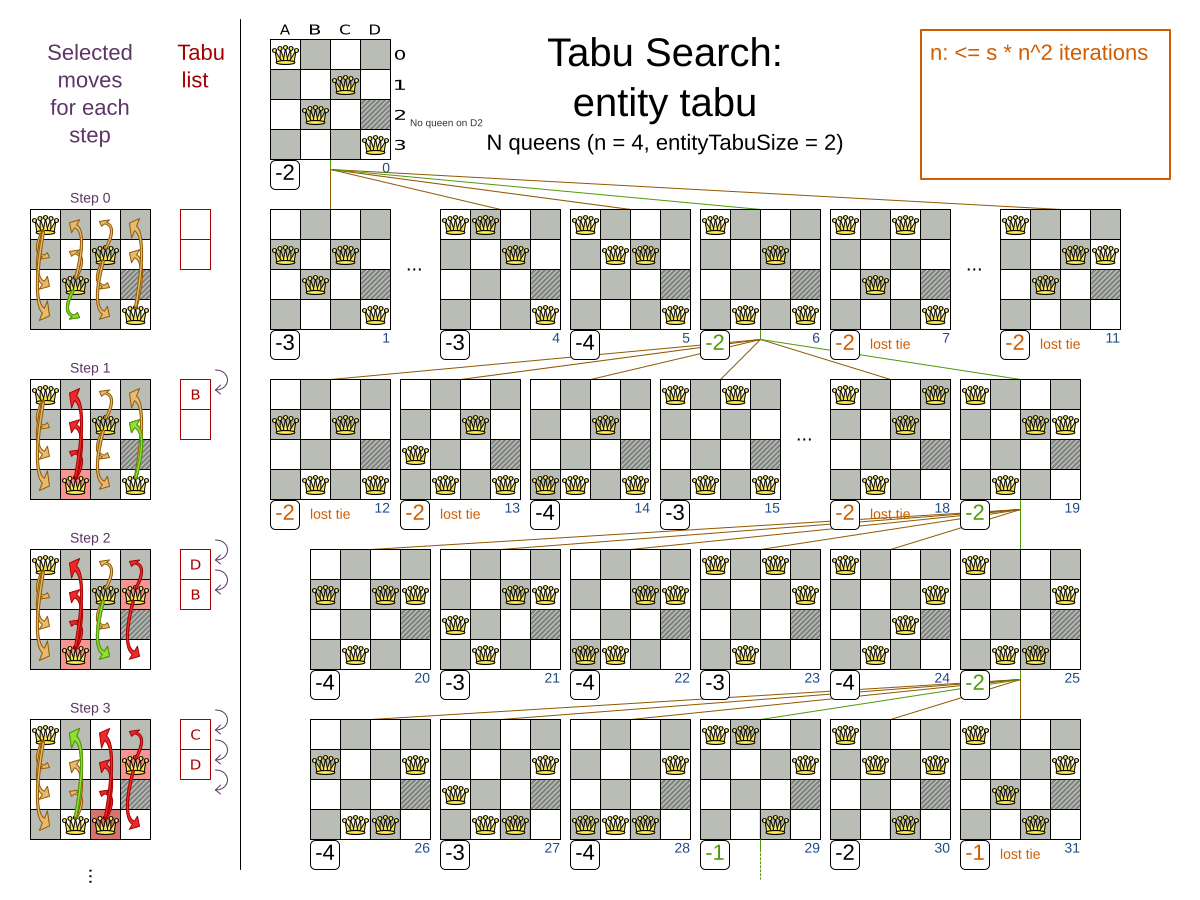
4.2. Configuration
Simplest configuration:
<localSearch>
<localSearchType>TABU_SEARCH</localSearchType>
</localSearch>When Tabu Search takes steps it creates one or more tabus. For a number of steps, it does not accept a move if that move breaks tabu. That number of steps is the tabu size. Advanced configuration:
<localSearch>
...
<acceptor>
<entityTabuSize>7</entityTabuSize>
</acceptor>
<forager>
<acceptedCountLimit>1000</acceptedCountLimit>
</forager>
</localSearch>|
A Tabu Search acceptor should be combined with a high |
Timefold Solver implements several tabu types:
-
Planning entity tabu (recommended) makes the planning entities of recent steps tabu. For example, for school timetabling it makes the recently moved lessons tabu. It’s recommended to start with this tabu type.
<acceptor> <entityTabuSize>7</entityTabuSize> </acceptor>To avoid hard coding the tabu size, configure a tabu ratio, relative to the number of entities, for example 2%:
<acceptor> <entityTabuRatio>0.02</entityTabuRatio> </acceptor> -
Planning value tabu makes the planning values of recent steps tabu. For example, for school timetablig it makes the recently assigned timeslots tabu.
<acceptor> <valueTabuSize>7</valueTabuSize> </acceptor>To avoid hard coding the tabu size, configure a tabu ratio, relative to the number of values, for example 2%:
<acceptor> <valueTabuRatio>0.02</valueTabuRatio> </acceptor> -
Move tabu makes recent steps tabu. It does not accept a move equal to one of those steps.
<acceptor> <moveTabuSize>7</moveTabuSize> </acceptor>
|
When using move tabu with custom moves,
make sure that the planning entities do not include planning variables in their |
Sometimes it’s useful to combine tabu types:
<acceptor>
<entityTabuSize>7</entityTabuSize>
<valueTabuSize>3</valueTabuSize>
</acceptor>If the tabu size is too small, the solver can still get stuck in a local optimum. On the other hand, if the tabu size is too large, the solver can be inefficient by bouncing off the walls. Use the Benchmarker to fine tweak your configuration.
5. Simulated annealing
5.1. Algorithm description
Simulated Annealing evaluates only a few moves per step, so it steps quickly. In the classic implementation, the first accepted move is the winning step. A move is accepted if it doesn’t decrease the score or - in case it does decrease the score - it passes a random check. The chance that a decreasing move passes the random check decreases relative to the size of the score decrement and the time the phase has been running (which is represented as the temperature).
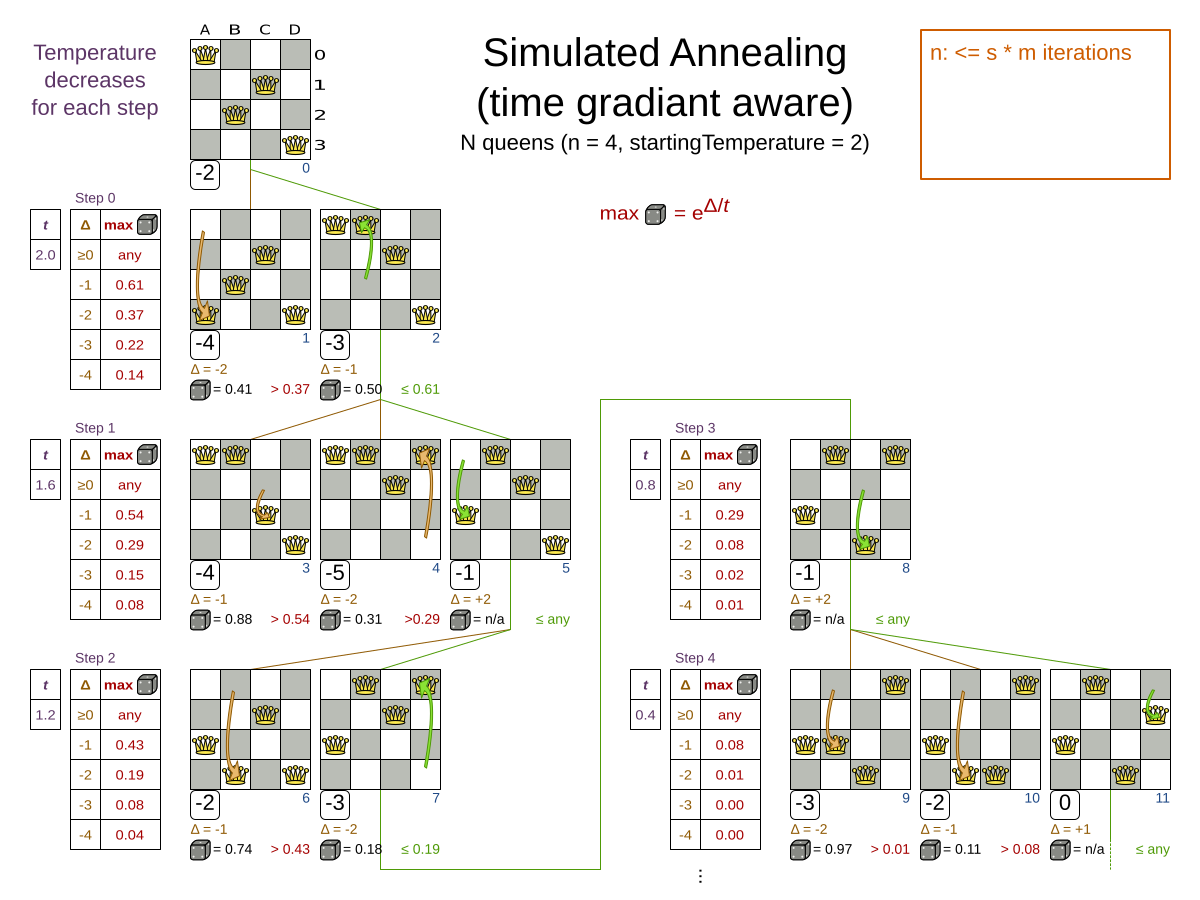
Simulated Annealing does not always pick the move with the highest score, neither does it evaluate many moves per step.
At least at first.
Instead, it gives non improving moves also a chance to be picked, depending on its score and the time gradient of the Termination.
In the end, it gradually turns into Hill Climbing, only accepting improving moves.
5.2. Configuration
Start with a simulatedAnnealingStartingTemperature set to the maximum score delta a single move can cause.
Use the Benchmarker to tweak the value.
Advanced configuration:
<localSearch>
...
<acceptor>
<simulatedAnnealingStartingTemperature>2hard/100soft</simulatedAnnealingStartingTemperature>
</acceptor>
<forager>
<acceptedCountLimit>1</acceptedCountLimit>
</forager>
</localSearch>Simulated Annealing should use a low acceptedCountLimit.
The classic algorithm uses an acceptedCountLimit of 1, but often 4 performs better.
Simulated Annealing can be combined with a tabu acceptor at the same time. That gives Simulated Annealing salted with a bit of Tabu. Use a lower tabu size than in a pure Tabu Search configuration.
<localSearch>
...
<acceptor>
<entityTabuSize>5</entityTabuSize>
<simulatedAnnealingStartingTemperature>2hard/100soft</simulatedAnnealingStartingTemperature>
</acceptor>
<forager>
<acceptedCountLimit>1</acceptedCountLimit>
</forager>
</localSearch>6. Late acceptance
6.1. Algorithm description
Late Acceptance (also known as Late Acceptance Hill Climbing) also evaluates only a few moves per step. A move is accepted if it does not decrease the score, or if it leads to a score that is at least the late score (which is the winning score of a fixed number of steps ago).
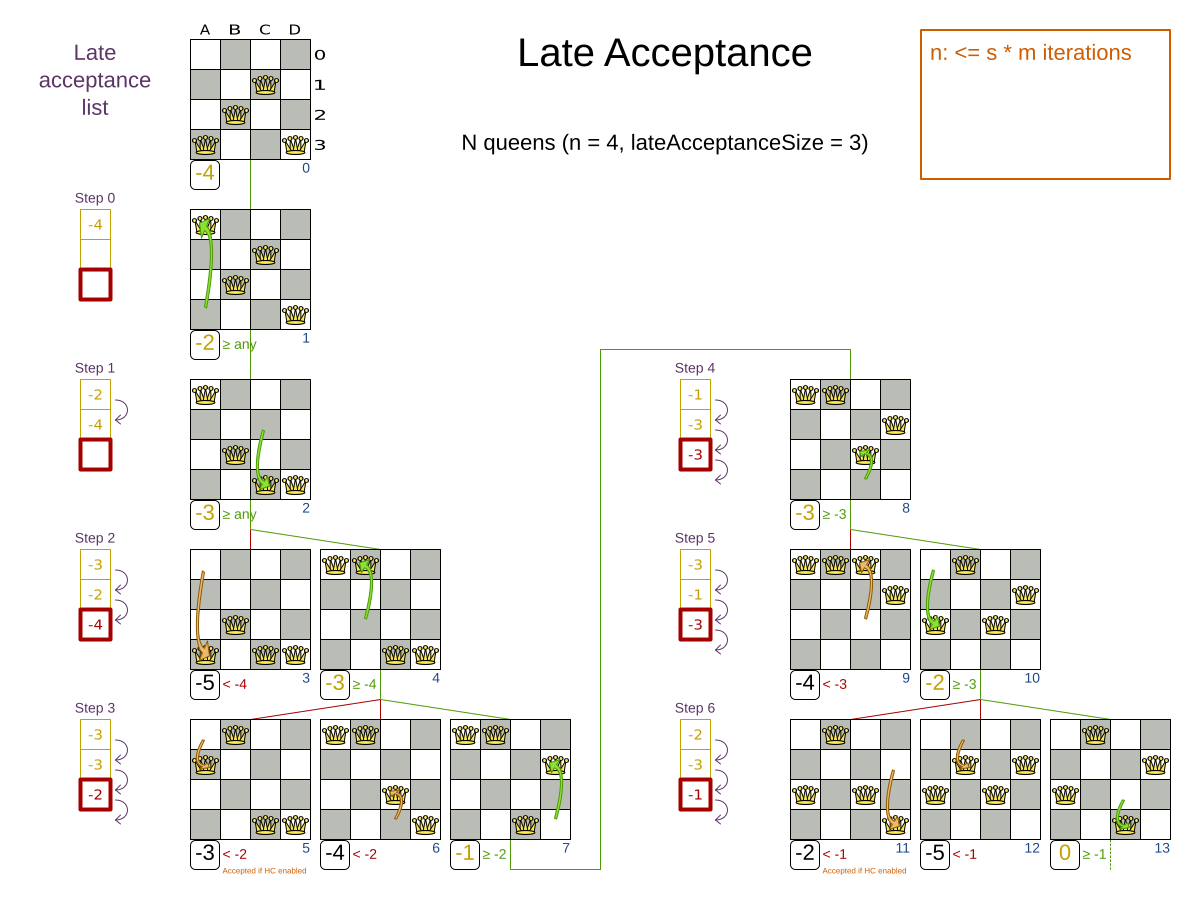
6.2. Configuration
Simplest configuration:
<localSearch>
<localSearchType>LATE_ACCEPTANCE</localSearchType>
</localSearch>Late Acceptance accepts any move that has a score which is higher than the best score of a number of steps ago.
That number of steps is the lateAcceptanceSize.
Advanced configuration:
<localSearch>
...
<acceptor>
<lateAcceptanceSize>400</lateAcceptanceSize>
</acceptor>
<forager>
<acceptedCountLimit>1</acceptedCountLimit>
</forager>
</localSearch>Late Acceptance should use a low acceptedCountLimit.
Late Acceptance can be combined with a tabu acceptor at the same time. That gives Late Acceptance salted with a bit of Tabu. Use a lower tabu size than in a pure Tabu Search configuration.
<localSearch>
...
<acceptor>
<entityTabuSize>5</entityTabuSize>
<lateAcceptanceSize>400</lateAcceptanceSize>
</acceptor>
<forager>
<acceptedCountLimit>1</acceptedCountLimit>
</forager>
</localSearch>7. Diversified Late acceptance
7.1. Algorithm description
Diversified Late Acceptance is similar to Late Acceptance, but it offers different acceptance and replacement strategies. A move is accepted if its score matches the current solution score or is better than the late score (which is the winning score of a fixed number of steps ago).
Diversified Late Acceptance was first proposed in Diversified Late Acceptance Search by M. Namazi, C. Sanderson, M. A. H. Newton, M. M. A. Polash, and A. Sattar
7.2. Configuration
Simplest configuration:
<solver xmlns="https://timefold.ai/xsd/solver">
<enablePreviewFeature>DIVERSIFIED_LATE_ACCEPTANCE</enablePreviewFeature>
...
<localSearch>
<localSearchType>DIVERSIFIED_LATE_ACCEPTANCE</localSearchType>
</localSearch>
</solver>The late elements list is updated as follows:
-
The current solution score is worse than the late score.
-
The current solution score is better than the late score and different from the previous one.
The size of the late elements list is typically smaller. Advanced configuration:
...
<localSearch>
...
<acceptor>
<lateAcceptanceSize>5</lateAcceptanceSize>
</acceptor>
<forager>
<acceptedCountLimit>1</acceptedCountLimit>
</forager>
</localSearch>|
The new acceptor is available as a preview feature
It may be subject to change and must be enabled in the solver configuration by setting: |
8. Great Deluge
8.1. Algorithm description
Great Deluge algorithm is similar to the Simulated Annealing algorithm, it evaluates only a few moves per steps, so it steps quickly. The first accepted move is the winning step. A move is accepted only if it is not lower than the score value (water level) that we are working with. It means Great Deluge is deterministic and opposite of Simulated Annealing has no randomization in it. The water level is increased after every step either about the fixed value or by percentual value. A gradual increase in water level gives Great Deluge more time to escape from local maxima.
8.2. Configuration
Simplest configuration:
<localSearch>
<localSearchType>GREAT_DELUGE</localSearchType>
</localSearch>Great Deluge takes as starting water level best score from construction heuristic and uses default rain speed ratio. Advanced configuration:
<localSearch>
...
<acceptor>
<greatDelugeWaterLevelIncrementRatio>0.00000005</greatDelugeWaterLevelIncrementRatio>
</acceptor>
<forager>
<acceptedCountLimit>1</acceptedCountLimit>
</forager>
</localSearch>Timefold Solver implements two water level increment options:
If greatDelugeWaterLevelIncrementScore is set, the water level is increased by a constant value.
<acceptor>
<greatDelugeWaterLevelIncrementScore>10</greatDelugeWaterLevelIncrementScore>
</acceptor>To avoid hard coding the water level increment, configure a greatDelugeWaterLevelIncrementRatio (recommended) when the water level is increased by percentual value, so there is no need to know the size of the problem or value of a scoring function.
<acceptor>
<greatDelugeWaterLevelIncrementRatio>0.00000005</greatDelugeWaterLevelIncrementRatio>
</acceptor>The algorithm takes as starting value the best score from the construction heuristic. Use the Benchmarker to fine-tune tweak your configuration.
9. Step counting hill climbing
9.1. Algorithm description
Step Counting Hill Climbing also evaluates only a few moves per step. For a number of steps, it keeps the step score as a threshold. A move is accepted if it does not decrease the score, or if it leads to a score that is at least the threshold score.
9.2. Configuration
Step Counting Hill Climbing accepts any move that has a score which is higher than a threshold score.
Every number of steps (specified by stepCountingHillClimbingSize), the threshold score is set to the step score.
<localSearch>
...
<acceptor>
<stepCountingHillClimbingSize>400</stepCountingHillClimbingSize>
</acceptor>
<forager>
<acceptedCountLimit>1</acceptedCountLimit>
</forager>
</localSearch>Step Counting Hill Climbing should use a low acceptedCountLimit.
Step Counting Hill Climbing can be combined with a tabu acceptor at the same time, similar as shown in the Late Acceptance section.
10. Strategic oscillation
10.1. Algorithm description
Strategic Oscillation is an add-on, which works especially well with Tabu Search. Instead of picking the accepted move with the highest score, it employs a different mechanism: If there’s an improving move, it picks it. If there’s no improving move however, it prefers moves which improve a softer score level, over moves which break a harder score level less.
10.2. Configuration
Configure a finalistPodiumType, such as in a Tabu Search configuration:
<localSearch>
...
<acceptor>
<entityTabuSize>7</entityTabuSize>
</acceptor>
<forager>
<acceptedCountLimit>1000</acceptedCountLimit>
<finalistPodiumType>STRATEGIC_OSCILLATION</finalistPodiumType>
</forager>
</localSearch>The following finalistPodiumTypes are supported:
-
HIGHEST_SCORE(default): Pick the accepted move with the highest score. -
STRATEGIC_OSCILLATION: Alias for the default strategic oscillation variant. -
STRATEGIC_OSCILLATION_BY_LEVEL: If there is an accepted improving move, pick it. If no such move exists, prefer an accepted move which improves a softer score level over one that doesn’t (even if it has a better harder score level). A move is improving if it’s better than the last completed step score. -
STRATEGIC_OSCILLATION_BY_LEVEL_ON_BEST_SCORE: LikeSTRATEGIC_OSCILLATION_BY_LEVEL, but define improving as better than the best score (instead of the last completed step score).
11. Variable neighborhood descent
11.1. Algorithm description
Variable Neighborhood Descent iteratively tries multiple move selectors in original order (depleting each selector entirely before trying the next one), picking the first improving move (which also resets the iterator back to the first move selector).
|
Despite that VND has a name that ends with descent (from the research papers), the implementation will ascend to a higher score (which is a better score). |
11.2. Configuration
Simplest configuration:
<localSearch>
<localSearchType>VARIABLE_NEIGHBORHOOD_DESCENT</localSearchType>
</localSearch>Advanced configuration:
<localSearch>
<unionMoveSelector>
<selectionOrder>ORIGINAL</selectionOrder>
<changeMoveSelector/>
<swapMoveSelector/>
...
</unionMoveSelector>
<acceptor>
<acceptorType>HILL_CLIMBING</acceptorType>
</acceptor>
<forager>
<pickEarlyType>FIRST_LAST_STEP_SCORE_IMPROVING</pickEarlyType>
</forager>
</localSearch>Variable Neighborhood Descent doesn’t scale well, but it is useful in some use cases with a very erratic score landscape.