Modeling planning problems
|
While we’ve simplified model creation with our constraint solver, it can still be complex and time-consuming. If rapid deployment is crucial, consider our pre-built models. Designed to tackle common optimization challenges, they integrate seamlessly through our REST API, enabling faster time-to-market. Explore our documentation and available models here. |
1. Introduction
Timefold Solver gives you access to a range of building blocks to model the domain of your planning problem. This page describes those building blocks in more detail.
If instead you are looking for guidance on how to create a good domain model, read the domain modeling guide.
|
If you have never tried Timefold Solver before, we recommend following our Getting Started guides for a practical introduction. |
A planning domain model typically consist of the following elements:
-
Planning entities are classes whose instances change during planning.
-
The properties of a planning entity that change during planning are called planning variables. The different types of planning variables are described below.
-
Genuine planning variables are assigned available planning values during solving.
-
Problem facts are classes that do not change during planning, but are used to validate constraints. Problem facts are often also used as planning values.
-
A planning solution class contains all the planning entities and problem facts, and often also provides the planning values that the solver can use during planning. It also contains the status of the solving process and the score of the planning problem.
In a school timetabling scenario, where lessons need to be assigned rooms and timeslots, we get this class diagram.
For this planning problem:
-
TimeslotandRoomare problem facts. -
Lessonis the planning entity, which has 2 planning variables:timeslotandroom. -
Timetableis the planning solution. It contains all theLessonplanning entity instances, and all possible planning values, which are instances ofRoomandTimeslotwhich can be assigned to the planning variables inLesson.
In Timefold Solver, all elements of the planning domain model are plain objects. Load them from a database, an XML file, a data repository, a REST service, a noSQL cloud, … (see integration): it doesn’t matter.
1.1. Types of planning variables
Planning variables are the properties of planning entities which the solver will change in its effort to find better solutions. There are 2 different types of planning variables we can distinguish: genuine and shadow planning variables.
1.1.1. Genuine planning variables
Genuine planning variables are variables to which the solver will assign planning values. There are 3 variants of genuine planning variables. The variants you use depends on the problem you are solving. For more detailed guidance on when to use which variant, read the domain modeling guide.
-
@PlanningVariable: contains a single planning value. Planning values can be assigned to multiple planning entities.
-
@PlanningListVariable: contains multiple planning values in a specific order. Planning values can only be assigned to a single planning entity.
-
Chained @PlanningVariable: allows planning entities to point to each other and form a chain. Planning values can only be part of a single chain.
A planning entity can contain a mix of these genuine variables, with some limitations.
1.1.2. Shadow planning variables
A shadow variable is a planning variable whose correct value can be deduced from the state of the genuine planning variables. From an optimization perspective, Timefold Solver effectively only optimizes genuine variables. Whenever a genuine variable is modified, the solver ensures that all dependent shadow variables are updated accordingly to maintain consistency.
Even though shadow variables violate the principle of normalization by definition, in some use cases it can be very practical to use a shadow variable, especially to express the constraints more naturally.
For example, in vehicle routing with time windows, the arrival time at a customer for a vehicle can be calculated based on the previously visited customers of that vehicle (and the known travel times between two locations).
When the customers for a vehicle change, the arrival time for each customer is automatically adjusted. For more information, see the vehicle routing domain model.
Depending on your use of @PlanningVariable, @PlanningListVariable or the Chained @PlanningVariable several built-in shadow variables are provided. These are documented in the details section of the respective genuine planning variables.
In addition, Timefold Solver also provides a way to implement shadow variables yourself.
2. Problem fact
A problem fact is any object with getters that does not change during planning. In school timetabling, the timeslots and rooms are problem facts:
-
Java
public class Timeslot {
DayOfWeek dayOfWeek;
LocalTime startTime;
LocalTime endTime;
...
}-
Java
public class Room {
String name;
...
}A problem fact can reference other problem facts:
-
Java
public class Course {
private String code;
private Teacher teacher; // Other problem fact
private int lectureSize;
private int minWorkingDaySize;
private List<Curriculum> curriculumList; // Other problem facts
private int studentSize;
// ... getters
}A problem fact class does not require any Timefold Solver specific code. For example, you can reuse your domain classes, which might have JPA or Jackson annotations.
|
Generally, better designed domain classes lead to simpler and more efficient score constraints.
Therefore, when dealing with a messy (denormalized) legacy system, it can sometimes be worthwhile to convert the messy domain model into a Timefold Solver specific model first.
For example: if your domain model has two Alternatively, you can sometimes also introduce a cached problem fact to enrich the domain model for planning only. |
2.1. @PlanningId
For some functionality (such as multi-threaded incremental solving and real-time planning), Timefold Solver needs to map problem facts and planning entities to an ID. Timefold Solver uses that ID to rebase a move from one thread’s solution state to another’s.
To enable such functionality, specify the @PlanningId annotation on the identification field or getter method,
for example on the database ID:
-
Java
public class Visit {
@PlanningId
private String username;
...
}A @PlanningId property must be:
-
Unique for that specific class
-
It does not need to be unique across different problem fact classes (unless in that rare case that those classes are mixed in the same value range or planning entity collection).
-
-
An instance of a type that implements
Object.hashCode()andObject.equals(). See the Javadoc on thejava.lang.Objectclass for details.-
It’s recommended to use the type
Integer,int,Long,long,StringorUUID.
-
-
Never
nullby the timeSolver.solve()is called.
3. Planning entity
3.1. Planning entity definition
A planning entity is a JavaBean (POJO) whose properties change during solving, for example a Lesson which has a Timeslot property.
A planning problem usually only has one planning entity class, for example the Lesson class.
A planning entity class needs to be annotated with the @PlanningEntity annotation.
The problem usually consists of multiple planning entities, which are instances of the planning entity class.
In school timetabling for example, each Lesson instance is a planning entity.
Each planning entity class has one or more planning variables (which can be genuine or shadows). It should also have one or more defining properties.
-
Java
@PlanningEntity
public class Lesson {
private String subject;
private String teacher;
private String studentGroup;
// Planning variables: changes during planning, between score calculations.
@PlanningVariable
private Timeslot timeslot;
@PlanningVariable
private Room room;
// ... getters and setters
}In the school timetabling example above, a Lesson is defined by its subject, teacher and a student group,
and has planning variables for its timeslot and room.
This means that `Lesson’s subject, teacher and student group never changes during solving,
while its timeslot and room do.
Planning entities need to be declared through the @PlanningEntity annotation on the class and in the solver configuration XML.
-
Java
@PlanningEntity
public class Lesson {
// Planning variables, getters, setters and fields excluded
}The solver configuration needs to declare each planning entity class:
<solver xmlns="https://timefold.ai/xsd/solver" xmlns:xsi="http://www.w3.org/2001/XMLSchema-instance"
xsi:schemaLocation="https://timefold.ai/xsd/solver https://timefold.ai/xsd/solver/solver.xsd">
...
<entityClass>org.acme.schooltimetabling.domain.Lesson</entityClass>
...
</solver>| When Timefold Solver is integrated in Quarkus or Spring, the XML file is optional. |
Some uses cases have multiple planning entity classes. For example: route freight and trains into railway network arcs, where each freight can use multiple trains over its journey and each train can carry multiple freights per arc.
3.2. Planning entity considerations
When implementing planning entities, take the following into account.
3.2.1. Do not create unnecessary planning entity classes
Having multiple planning entity classes directly raises the implementation complexity of your use case. Consequently, this will also increase the time it takes Timefold Solver to find optimized solutions. If possible, avoid creating planning entity classes and use one of the other available mechanisms instead.
For example, do not create a planning entity class to hold the total free time of a teacher, which needs to be kept up to date as the Lecture planning entities change.
Instead, calculate the free time in the score constraints (or as a shadow variable).
If historic data needs to be considered too, then create a problem fact to hold the total of the historic assignments up to, but not including, the planning window (so that it does not change when a planning entity changes) and let the score constraints take it into account.
3.2.2. Keep planning entity hashCode() implementations constant
Planning entity hashCode() implementations must remain constant.
Therefore, entity hashCode() implementations must not depend on any planning variables, as these change during solving.
Pay special attention when using data structures with auto-generated hashCode() as entities,
such as Kotlin data classes or Lombok’s @EqualsAndHashCode.
3.3. Planning entity sorting
Some optimization algorithms are more efficient when planning entities are sorted based on a specific metric, which helps estimate the relative difficulty of each planning entity. For example: in bin packing bigger items are harder to fit.
|
Do not try to use planning entity order to implement a business constraint. It will not affect the score function: if we have infinite solving time, the returned solution will be the same. To attain a schedule in which certain entities are scheduled earlier in the schedule, add a score constraint to change the score function so it prefers such solutions. Only consider adding planning entity sort order if it can make the solver more efficient. |
To allow the heuristics to take advantage of that domain specific information,
set a comparatorClass to the @PlanningEntity annotation:
@PlanningEntity(comparatorClass = VisitComparator.class)
public class Visit {
// ...
}public class VisitComparator implements Comparator<Visit> {
public int compare(Visit a, Visit b) {
return new CompareToBuilder()
.append(a.getServiceDuration(), b.getServiceDuration())
.append(a.getId(), b.getId())
.toComparison();
}
}Alternatively, you can also set a comparatorFactoryClass to the @PlanningEntity annotation,
so that you have access to the rest of the problem facts from the solution too.
See sorted selection for more information.
|
Entities should be sorted in ascending order: "easy" entities are lower, "difficult" entities are higher. For example, in bin packing: small item < medium item < big item. Although most algorithms start in descending order, they just reverse the ordering. |
None of the current planning variable states should be used to compare planning entities.
During Construction Heuristics, those variables are likely to be null anyway.
For example, a Lesson's timeslot variable should not be used.
3.4. When is a planning entity considered initialized
A planning entity is considered initialized in either of the following cases:
-
No genuine planning variable is set to
null. -
Genuine planning variable is set to
null, but it allows unassigned values. -
No possible value for a list variable is left unassigned to any one of the genuine entities, unless it allows unassigned values.
| It follows that, if unassigned values are allowed, a planning entity is always considered initialized. |
Local Search will refuse to start when it encounters an uninitialized entity in your planning solution. Run Construction Heuristics before Local Search to get a good starting solution.
4. Basic planning variable (@PlanningVariable)
A basic variable is a JavaBean property (so a getter and setter) on a planning entity. It is a genuine planning variable, so it points to a planning value, which changes during planning.
In the example below, a Lesson's timeslot property is a basic planning variable.
Note that even though a Lesson's timeslot property changes to another Timeslot during planning,
no Timeslot instance itself is changed.
Normally planning variables are genuine, but advanced cases can also have shadows.
A basic planning variable getter needs to be annotated with the @PlanningVariable annotation,
optionally with a non-empty valueRangeProviderRefs property.
@PlanningEntity
public class Lesson {
...
private Timeslot timeslot;
@PlanningVariable
public Timeslot getTimeslot() {
return timestlot;
}
public void setTimeslot(Timeslot timeslot) {
this.timestlot = timeslot;
}
...
}The optional valueRangeProviderRefs property defines what are the possible planning values for this planning variable.
It references one or more @ValueRangeProvider id's.
If none are provided, Timefold Solver will attempt to auto-detect matching @ValueRangeProviders.
|
A @PlanningVariable annotation needs to be on a member in a class with a @PlanningEntity annotation. It is ignored on parent classes or subclasses without that annotation. |
Annotating the field instead of the property works too:
-
Java
@PlanningEntity
public class Lesson {
...
@PlanningVariable
private Timeslot timeslot;
...
}|
For more advanced planning variables used to model precedence relationships, see planning list variable and chained planning variable. |
4.1. Allowing unassigned values
By default, an initialized planning variable cannot be null,
so an initialized solution will never use null for any of its planning variables.
In an over-constrained use case, this can be counterproductive.
For example: in task assignment with too many tasks for the workforce,
we would rather leave low priority tasks unassigned instead of assigning them to an overloaded worker.
To allow an initialized planning variable to be null, set allowsUnassigned to true:
-
Java
@PlanningVariable(..., allowsUnassigned = true)
public Worker getWorker() {
return worker;
}|
Constraint Streams filter out planning entities with a |
Timefold Solver will automatically add the value null to the value range.
There is no need to add null in a collection provided by a ValueRangeProvider.
|
Using a planning variable with unassigned values implies
that your score calculation is responsible for punishing (or even rewarding) variables with a Failure to penalize unassigned variables can cause a solution with all variables unassigned to be the best solution.
See the overconstrained planning with |
Repeated planning
(especially real-time planning)
does not mix well with a planning variable that allows unassigned values.
Every time the Solver starts or a problem fact change is made,
the Construction Heuristics
will try to initialize all the null variables again, which can be a huge waste of time.
One way to deal with this is to filter the entity selector of the placer in the construction heuristic.
<solver xmlns="https://timefold.ai/xsd/solver" xmlns:xsi="http://www.w3.org/2001/XMLSchema-instance"
xsi:schemaLocation="https://timefold.ai/xsd/solver https://timefold.ai/xsd/solver/solver.xsd">
...
<constructionHeuristic>
<queuedEntityPlacer>
<entitySelector id="entitySelector1">
<filterClass>...</filterClass>
</entitySelector>
</queuedEntityPlacer>
...
<changeMoveSelector>
<entitySelector mimicSelectorRef="entitySelector1" />
</changeMoveSelector>
...
</constructionHeuristic>
...
</solver>4.2. Basic variable shadow variables
When a planning entity uses basic planning variables, you can use the following built-in annotation to derive shadow variables from that genuine planning variable.
-
@InverseRelationShadowVariable: for mapping bidirectional relationships.
If the built-in shadow variable annotations are insufficient, @ShadowVariable can be used to create custom handlers.
4.2.1. Inverse relation shadow variable
Two variables are bi-directional if their instances always point to each other,
unless one side points to null and the other side does not exist.
So if A references B, then B references A.
For basic planning variables, the bi-directional relationship must be a many-to-one relationship. To map a bi-directional relationship between two planning variables, annotate the source side (which is the genuine side) as a normal planning variable:
-
Java
@PlanningEntity
public class Lesson {
@PlanningVariable(...)
public Timeslot timeslot;
...
}And then annotate the other side (which is the shadow side)
with a @InverseRelationShadowVariable annotation on a Collection (usually a Set or List) property:
-
Java
@PlanningEntity
public class Timeslot {
@InverseRelationShadowVariable(sourceVariableName = "timeslot")
public List<Lesson> lessons;
...
}The sourceVariableName property is the name of the genuine planning variable on the return type of the getter
(so the name of the genuine planning variable on the other side).
|
The shadow property, which is |
5. Planning list variable (VRP, Task assigning, …)
Use the planning list variable to model problems where the goal is to distribute a number of workload elements among limited resources in a specific order. This includes, for example, vehicle routing, traveling salesman, task assigning, and similar problems.
|
Use a chained planning variable instead of a planning list variable, if you need any of the following planning techniques:
|
For example, the vehicle routing problem can be modeled as follows:
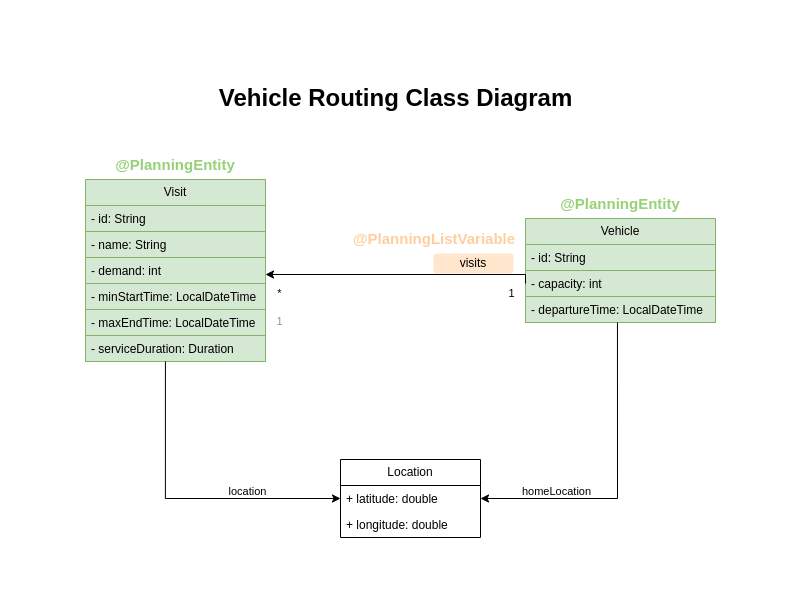
This model is closer to the reality than the chained model. Each vehicle has a list of customers to go to in the order given by the list. And indeed, the object model matches the natural language description of the problem:
-
Java
@PlanningEntity
class Vehicle {
int capacity;
Depot depot;
@PlanningListVariable
List<Customer> customers = new ArrayList<>();
}Planning list variable can be used if the domain meets the following criteria:
-
There is a one-to-many relationship between the planning entity and the planning value.
-
The order in which planning values are assigned to an entity’s list variable is significant.
-
Each planning value is assigned to exactly one planning entity. No planning value may appear in multiple entities.
5.1. Allowing unassigned values
By default, all planning values have to be assigned to exactly one list variable across the entire planning model. In an over-constrained use case, this can be counterproductive. For example: in task assignment with too many tasks for the workforce, we would rather leave low priority tasks unassigned instead of assigning them to an overloaded worker.
To allow a planning value to be unassigned, set allowsUnassignedValues to true:
-
Java
@PlanningListVariable(allowsUnassignedValues = true)
public List<Customer> getCustomers() {
return customers;
}|
Constraint Streams filter out unassigned planning values by default. Use forEachIncludingUnassigned() to avoid such unwanted behaviour. Using a planning list variable with unassigned values implies that your score calculation is responsible for punishing (or even rewarding) these unassigned values. Failure to penalize unassigned values can cause a solution with all values unassigned to be the best solution.
See the overconstrained planning with |
Repeated planning
(especially real-time planning)
does not mix well with a planning list variable that allows unassigned values.
Every time the Solver starts or a problem fact change is made,
the Construction Heuristics
will try to initialize all the null variables again, which can be a huge waste of time.
One way to deal with this is to filter the entity selector of the placer in the construction heuristic.
<solver xmlns="https://timefold.ai/xsd/solver" xmlns:xsi="http://www.w3.org/2001/XMLSchema-instance"
xsi:schemaLocation="https://timefold.ai/xsd/solver https://timefold.ai/xsd/solver/solver.xsd">
...
<constructionHeuristic>
<queuedValuePlacer>
<valueSelector id="selector1">
<filterClass>...</filterClass>
</valueSelector>
</queuedValuePlacer>
...
<listChangeMoveSelector>
<valueSelector mimicSelectorRef="selector1" />
</listChangeMoveSelector>
...
</constructionHeuristic>
...
</solver>5.2. List variable shadow variables
When the planning entity uses a list variable, you can use the following built-in annotations to derive shadow variables from that genuine planning variable.
-
@InverseRelationShadowVariable: Used to get the planning entity containing the planning variable list to which a planning value is assigned;
-
@IndexShadowVariable: Used to get the index of a planning value’s position it’s assigned planning variable list;
-
@PreviousElementShadowVariable: Used to get a planning value’s predecessor in its assigned planning variable list;
-
@NextElementShadowVariable: Used to get a planning value’s successor in its assigned planning variable list;
-
@CascadingUpdateShadowVariable: Used to update a set of connected elements;
If the built-in shadow variable annotations are insufficient, @ShadowVariable can be used to create custom handlers.
5.2.1. Inverse relation shadow variable
Use the @InverseRelationShadowVariable annotation to establish bi-directional relationship between the entity and the elements assigned to its list variable.
The type of the inverse shadow variable is the planning entity itself
because there is a one-to-many relationship between the entity and the element classes.
The planning entity side has a genuine list variable:
-
Java
@PlanningEntity
public class Vehicle {
@PlanningListVariable
public List<Customer> getCustomers() {
return customers;
}
public void setCustomers(List<Customer> customers) {...}
}On the element side:
-
Annotate the class with
@PlanningEntityto make it a shadow planning entity. -
Register this class as a planning entity, otherwise Timefold Solver won’t detect it and the shadow variable won’t update.
-
Create a property with the genuine planning entity type.
-
Annotate it with
@InverseRelationShadowVariableand setsourceVariableNameto the name of the genuine planning list variable.
-
Java
@PlanningEntity
public class Customer {
@InverseRelationShadowVariable(sourceVariableName = "customers")
public Vehicle getVehicle() {
return vehicle;
}
public void setVehicle(Vehicle vehicle) {...}
}5.2.2. Index shadow variable
While the @InverseRelationShadowVariable allows to establish the bi-directional relationship between the entity
and the elements assigned to its list variable,
@IndexShadowVariable provides a pointer into the entity’s list variable where the element is assigned.
The planning entity side has a genuine list variable:
-
Java
@PlanningEntity
public class Vehicle {
@PlanningListVariable
public List<Customer> getCustomers() {
return customers;
}
public void setCustomers(List<Customer> customers) {...}
}On the element side:
-
Annotate the class with
@PlanningEntityto make it a shadow planning entity. -
Register this class as a planning entity, otherwise Timefold Solver won’t detect it and the shadow variable won’t update.
-
Create a property which returns an
Integer.Integeris required instead ofint, as the index may benullif the element is not yet assigned to the list variable. -
Annotate it with
@IndexShadowVariableand setsourceVariableNameto the name of the genuine planning list variable.
-
Java
@PlanningEntity
public class Customer {
@IndexShadowVariable(sourceVariableName = "customers")
public Integer getIndexInVehicle() {
return indexInVehicle;
}
}5.2.3. Previous and next element shadow variable
Use @PreviousElementShadowVariable or @NextElementShadowVariable to get a reference to an element that is assigned to the same entity’s list variable one index lower (previous element) or one index higher (next element).
The previous and next element shadow variables may be null even in a fully initialized solution.
The first element’s previous shadow variable is null and the last element’s next shadow variable is null.
|
The planning entity side has a genuine list variable:
-
Java
@PlanningEntity
public class Vehicle {
@PlanningListVariable
public List<Customer> getCustomers() {
return customers;
}
public void setCustomers(List<Customer> customers) {...}
}On the element side:
-
Java
@PlanningEntity
public class Customer {
@PreviousElementShadowVariable(sourceVariableName = "customers")
public Customer getPreviousCustomer() {
return previousCustomer;
}
public void setPreviousCustomer(Customer previousCustomer) {...}
@NextElementShadowVariable(sourceVariableName = "customers")
public Customer getNextCustomer() {
return nextCustomer;
}
public void setNextCustomer(Customer nextCustomer) {...}5.3. Updating tail chains
The annotation @CascadingUpdateShadowVariable enables updates a set of connected elements.
Timefold Solver triggers a user-defined logic after all events are processed.
Hence, the related listener is the final one executed during the event lifecycle.
Moreover,
it automatically propagates changes to the subsequent elements in the list
when the value of the related shadow variable changes.
The planning entity side has a genuine list variable:
-
Java
@PlanningEntity
public class Vehicle {
@PlanningListVariable
public List<Customer> getCustomers() {
return customers;
}
public void setCustomers(List<Customer> customers) {...}
}On the element side:
-
Java
@PlanningEntity
public class Customer {
@InverseRelationShadowVariable(sourceVariableName = "customers")
private Vehicle vehicle;
@PreviousElementShadowVariable(sourceVariableName = "customers")
private Customer previousCustomer;
@CascadingUpdateShadowVariable(targetMethodName = "updateArrivalTime")
private LocalDateTime arrivalTime;
...
public void updateArrivalTime() {...}The targetMethodName refers to the user-defined logic that updates the annotated shadow variable.
The method must be implemented in the defining entity class, be non-static, and not include any parameters.
In the previous example,
the cascade update listener calls updateArrivalTime after all shadow variables have been updated,
including vehicle and previousCustomer.
It then automatically calls updateArrivalTime for the subsequent customers
and stops when the arrivalTime value does not change after running target method
or when it reaches the end.
|
A user-defined logic can only change shadow variables. Changing a genuine planning variable or a problem fact will result in score corruption. |
|
When distinct target methods are used by separate |
5.3.1. Multiple sources
If the user-defined logic requires updating multiple shadow variables,
apply the @CascadingUpdateShadowVariable to all shadow variables.
-
Java
@PlanningEntity
public class Customer {
@PreviousElementShadowVariable(sourceVariableName = "customers")
private Customer previousCustomer;
@NextElementShadowVariable(sourceVariableName = "customers")
private Customer nextCustomer;
@CascadingUpdateShadowVariable(targetMethodName = "updateWeightAndArrivalTime")
private LocalDateTime arrivalTime;
@CascadingUpdateShadowVariable(targetMethodName = "updateWeightAndArrivalTime")
private Integer weightAtVisit;
...
public void updateWeightAndArrivalTime() {...}Timefold Solver triggers the user-defined logic in updateWeightAndArrivalTime at the end of the event lifecycle.
It stops when both arrivalTime and weightAtVisit values do not change or when it reaches the end.
6. Planning value and planning value range
6.1. Planning value
A planning value is a possible value for a genuine planning variable.
Usually, a planning value is a problem fact, but it can also be any object, for example an Integer.
It can even be another planning entity or even an interface implemented by both a planning entity and a problem fact.
|
Primitive types (such as |
A planning value range is the set of possible planning values for a planning variable. Planning value ranges need to come from a finite collection.
6.2. Planning value range provider
6.2.1. Overview
The value range of a planning variable is defined with the @ValueRangeProvider annotation.
A @ValueRangeProvider may carry a property id, which is referenced by the @PlanningVariable's property valueRangeProviderRefs.
This annotation can be located on two types of methods:
-
On the Solution: All planning entities share the same value range.
-
On the planning entity: The value range differs per planning entity. This is less common.
|
A |
The return type of that method can be three types:
-
Collection: The value range is defined by aCollection(usually aList) of its possible values. -
Array: The value range is defined by an array of its possible values.
-
CountableValueRange: The value range is defined by its bounds. This is less common.
6.2.2. ValueRangeProvider on the solution
All instances of the same planning entity class share the same set of possible planning values for that planning variable. This is the most common way to configure a value range.
The @PlanningSolution implementation has a method that returns a Collection (or a CountableValueRange).
Any value from that Collection is a possible planning value for this planning variable.
-
Java
@PlanningVariable
public Timeslot getTimeslot() {
return timeslot;
}@PlanningSolution
public class Timetable {
...
@ValueRangeProvider
public List<Timeslot> getTimeslots() {
return timeslots;
}
}|
That |
Annotating the field instead of the property works too:
-
Java
@PlanningSolution
public class Timetable {
...
@ValueRangeProvider
private List<Timeslot> timeslots;
}6.2.3. ValueRangeProvider on the Planning Entity
Each planning entity has its own value range (a set of possible planning values) for the planning variable. For example, if a teacher can never teach in a room that does not belong to their department, lectures of that teacher can limit their room value range to the rooms of their department.
-
Java
@PlanningVariable
public Room getRoom() {
return room;
}
@ValueRangeProvider
public List<Room> getPossibleRoomList() {
return getCourse().getTeacher().getDepartment().getRoomList();
}Never use this to enforce a soft constraint (or even a hard constraint when the problem might not have a feasible solution). For example: Unless there is no other way, a teacher cannot teach in a room that does not belong to their department. In this case, the teacher should not be limited in their room value range (because sometimes there is no other way).
|
By limiting the value range specifically of one planning entity, you are effectively creating a built-in hard constraint. This can have the benefit of severely lowering the number of possible solutions; however, it can also take away the freedom of the optimization algorithms to temporarily break that constraint in order to escape from a local optimum. |
A planning entity should not use other planning entities to determine its value range. That would only try to make the planning entity solve the planning problem itself and interfere with the optimization algorithms.
Every entity has its own List instance, unless multiple entities have the same value range.
For example, if teacher A and B belong to the same department, they use the same List<Room> instance.
Furthermore, each List contains a subset of the same set of planning value instances.
For example, if department A and B can both use room X, then their List<Room> instances contain the same Room instance.
|
A |
|
A |
The value range annotated method can also be defined with a single parameter, which must be of the same type as the solution class. The method will have access to the current solution and allow for the dynamic generation of a list of values.
-
Java
@PlanningVariable
public Room getRoom() {
return room;
}
@ValueRangeProvider
public List<Room> getPossibleRoomListWithSolution(Timetable timetable) {
return timetable.getRoomListFor(this);
}|
A |
6.2.4. Referencing ValueRangeProviders
There are two ways how to match a planning variable to a value range provider. The simplest way is to have value range provider auto-detected. Another way is to explicitly reference the value range provider.
Anonymous ValueRangeProviders
We already described the first approach.
By not providing any valueRangeProviderRefs on the @PlanningVariable annotation,
Timefold Solver will go over every @ValueRangeProvider-annotated method or field which does not have an id property set,
and will match planning variables with value ranges where their types match.
In the following example,
the planning variable car will be matched to the value range returned by getCompanyCarList(),
as they both use the Car type.
It will not match getPersonalCarList(),
because that value range provider is not anonymous; it specifies an id.
-
Java
@PlanningVariable
public Car getCar() {
return car;
}
@ValueRangeProvider
public List<Car> getCompanyCarList() {
return companyCarList;
}
@ValueRangeProvider(id = "personalCarRange")
public List<Car> getPersonalCarList() {
return personalCarList;
}Automatic matching also accounts for polymorphism.
In the following example,
the planning variable car will be matched to getCompanyCarList() and getPersonalCarList(),
as both CompanyCar and PersonalCar are Cars.
It will not match getAirplanes(),
as an Airplane is not a Car.
-
Java
@PlanningVariable
public Car getCar() {
return car;
}
@ValueRangeProvider
public List<CompanyCar> getCompanyCarList() {
return companyCarList;
}
@ValueRangeProvider
public List<PersonalCar> getPersonalCarList() {
return personalCarList;
}
@ValueRangeProvider
public List<Airplane> getAirplanes() {
return airplaneList;
}Explicitly referenced ValueRangeProviders
In more complicated cases where auto-detection is not sufficient or where clarity is preferred over simplicity, value range providers can also be referenced explicitly.
In the following example,
the car planning variable will only be matched to value range provided by methods getCompanyCarList().
-
Java
@PlanningVariable(valueRangeProviderRefs = {"companyCarRange"})
public Car getCar() {
return car;
}
@ValueRangeProvider(id = "companyCarRange")
public List<CompanyCar> getCompanyCarList() {
return companyCarList;
}
@ValueRangeProvider(id = "personalCarRange")
public List<PersonalCar> getPersonalCarList() {
return personalCarList;
}Explicitly referenced value range providers can also be combined, for example:
-
Java
@PlanningVariable(valueRangeProviderRefs = { "companyCarRange", "personalCarRange" })
public Car getCar() {
return car;
}
@ValueRangeProvider(id = "companyCarRange")
public List<CompanyCar> getCompanyCarList() {
return companyCarList;
}
@ValueRangeProvider(id = "personalCarRange")
public List<PersonalCar> getPersonalCarList() {
return personalCarList;
}6.2.5. ValueRangeFactory
Instead of a Collection, you can also return CountableValueRange, built by the ValueRangeFactory:
-
Java
@ValueRangeProvider
public CountableValueRange<Integer> getDelayRange() {
return ValueRangeFactory.createIntValueRange(0, 5000);
}A CountableValueRange uses far less memory, because it only holds the bounds.
In the example above, a Collection would need to hold all 5000 ints, instead of just the two bounds.
Furthermore, an incrementUnit can be specified, for example if you have to buy stocks in units of 200 pieces:
-
Java
@ValueRangeProvider
public CountableValueRange<Integer> getStockAmountRange() {
// Range: 0, 200, 400, 600, ..., 9999600, 9999800, 10000000
return ValueRangeFactory.createIntValueRange(0, 10000000, 200);
}The ValueRangeFactory has creation methods for several value class types:
-
boolean: A boolean range. -
int: A 32bit integer range. -
long: A 64bit integer range. -
BigInteger: An arbitrary-precision integer range. -
BigDecimal: A decimal point range. By default, the increment unit is the lowest non-zero value in the scale of the bounds. -
Temporal(such asLocalDate,LocalDateTime, …): A time range.
6.3. Planning value sorting
Some optimization algorithms work a bit more efficiently if the planning values are sorted according to a given metric, which means they are more likely to satisfy a planning entity requirement. For example: in bin packing bigger containers are more likely to fit an item.
|
Do not try to use planning value order to implement a business constraint. It will not affect the score function: if we have infinite solving time, the returned solution will be the same. To affect the score function, add a score constraint. Only consider adding planning value sort order if it can make the solver more efficient. |
To allow the heuristics to take advantage of that domain specific information,
set a comparatorClass to the @PlanningVariable annotation:
@PlanningVariable(..., comparatorClass = VehicleComparator.class)
public Vehicle getVehicle() {
return vehicle;
}public class VehicleComparator implements Comparator<Vehicle> {
public int compare(Vehicle a, Vehicle b) {
return new CompareToBuilder()
.append(a.getCapacity(), b.getCapacity())
.append(a.getId(), b.getId())
.toComparison();
}
}|
If you have multiple planning value classes in the same value range,
the |
If the model uses a list variable,
the setting process is similar,
and the property comparatorClass must be specified in the @PlanningListVariable annotation:
@PlanningListVariable(..., comparatorClass = CustomerComparator.class)
List<Customer> customers = new ArrayList<>();public class CustomerComparator implements Comparator<Customer> {
public int compare(Customer a, Customer b) {
return new CompareToBuilder()
.append(a.getPriority(), b.getPriority())
.append(a.getId(), b.getId())
.toComparison();
}
}Alternatively,
you can also set a comparatorFactoryClass to the @PlanningVariable or @PlanningListVariable annotations,
so you have access to the rest of the problem facts from the solution too.
See sorted selection for more information.
|
Values should be sorted in ascending order: "weaker" values are lower, and "stronger" values are higher. In bin packing, small container < medium container < big container. |
None of the current planning variable state in any of the planning entities should be used to compare planning values.
During construction heuristics, those variables are likely to be null.
For example, none of the timeslot variables of any Lesson may be used to determine the order of a Timeslot.
7. Chained planning variable (TSP, VRP, …)
Chained planning variable is one way to implement the Chained Through Time pattern. This pattern is used for some use cases, such as TSP and vehicle routing. Only use the chained planning variable to implement this pattern if you plan to use some of the advanced planning features that are not yet supported by the planning list variable.
Chained planning variable allows the planning entities to point to each other and form a chain. By modeling the problem as a set of chains (instead of a set of trees/loops), the search space is heavily reduced.
A planning variable that is chained either:
-
Directly points to a problem fact (or planning entity), which is called an anchor.
-
Points to another planning entity with the same planning variable, which recursively points to an anchor.
Here are some examples of valid and invalid chains:
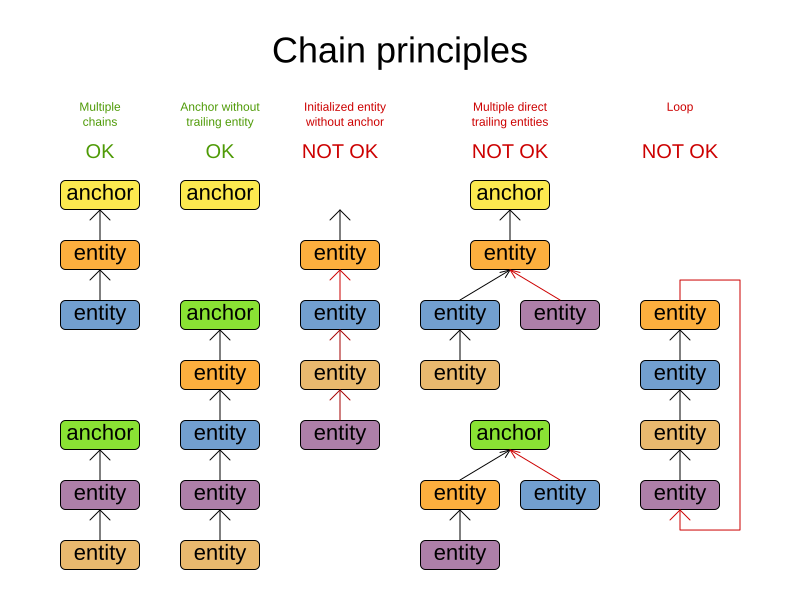
7.1. Chained variable considerations
Every initialized planning entity is part of an open-ended chain that begins from an anchor. A valid model means that:
-
A chain is never a loop. The tail is always open.
-
Every chain always has exactly one anchor. The anchor is never an instance of the planning entity class that contains the chained planning variable.
-
A chain is never a tree, it is always a line. Every anchor or planning entity has at most one trailing planning entity.
-
Every initialized planning entity is part of a chain.
-
An anchor with no planning entities pointing to it, is also considered a chain.
|
If your constraints dictate a closed chain, model it as an open-ended chain (which is easier to persist in a database) and implement a score constraint for the last entity back to the anchor. |
The optimization algorithms and built-in Moves do chain correction to guarantee that the model stays valid:
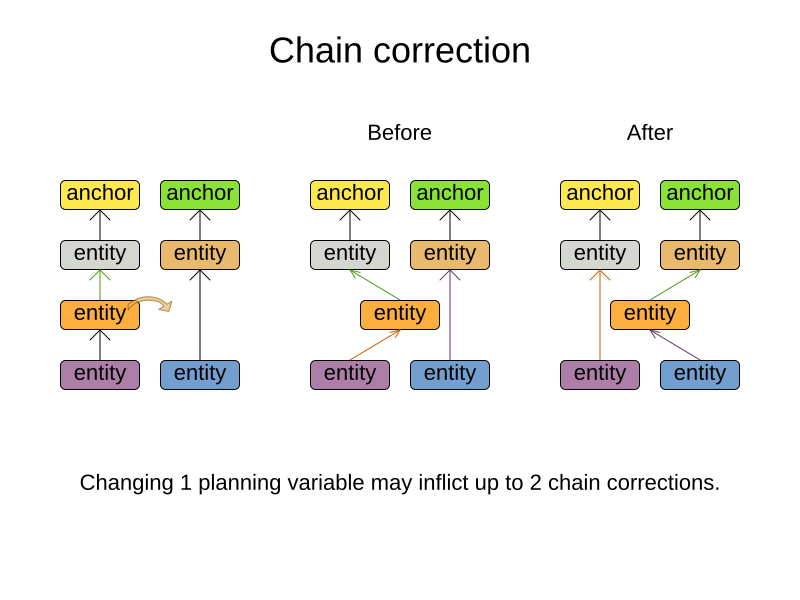
|
A custom |
For example, in TSP the anchor is a Domicile (in vehicle routing it is Vehicle):
-
Java
public class Domicile ... implements Standstill {
...
public City getCity() {...}
}The anchor (which is a problem fact) and the planning entity implement a common interface, for example TSP’s Standstill:
-
Java
public interface Standstill {
City getCity();
}That interface is the return type of the planning variable.
Furthermore, the planning variable is chained.
For example, TSP’s Visit would look like this:
-
Java
@PlanningEntity
public class Visit ... implements Standstill {
...
public City getCity() {...}
@PlanningVariable(graphType = PlanningVariableGraphType.CHAINED)
public Standstill getPreviousStandstill() {
return previousStandstill;
}
public void setPreviousStandstill(Standstill previousStandstill) {
this.previousStandstill = previousStandstill;
}
}|
Two value range providers are usually combined:
Since |
|
Despite using the same base annotation as basic planning variables, chained planning variables are not compatible with the |
7.2. Chained variable shadow variables
When a planning entity uses a chained variable, you can use the following built-in annotations to derive shadow variables from that genuine planning variable.
-
@InverseRelationShadowVariable: Used to get the planning entity containing the chained planning variable to which a planning value is assigned;
-
@AnchorShadowVariable: Used to get the planning entity containing the planning variable list to which a planning value is assigned;
If the built-in shadow variable annotations are insufficient, @ShadowVariable can be used to create custom handlers.
7.2.1. Bi-directional variable (inverse relation shadow variable)
Two variables are bi-directional if their instances always point to each other,
unless one side points to null and the other side does not exist.
So if A references B, then B references A.
For a chained planning variable, the bi-directional relationship is always a one-to-one relationship. In that case, the genuine side looks like this:
-
Java
@PlanningEntity
public class Customer ... {
@PlanningVariable(graphType = PlanningVariableGraphType.CHAINED, ...)
public Standstill getPreviousStandstill() {
return previousStandstill;
}
public void setPreviousStandstill(Standstill previousStandstill) {...}
}And the shadow side looks like this:
-
Java
@PlanningEntity
public class Standstill {
@InverseRelationShadowVariable(sourceVariableName = "previousStandstill")
public Customer getNextCustomer() {
return nextCustomer;
}
public void setNextCustomer(Customer nextCustomer) {...}
}|
The input planning problem of a |
7.2.2. Anchor shadow variable
An anchor shadow variable is the anchor of a chained variable.
Annotate the anchor property as a @AnchorShadowVariable annotation:
-
Java
@PlanningEntity
public class Customer {
@AnchorShadowVariable(sourceVariableName = "previousStandstill")
public Vehicle getVehicle() {...}
public void setVehicle(Vehicle vehicle) {...}
}The sourceVariableName property is the name of the chained variable on the same entity class.
8. Mixed models
The following planning entity defines two genuine variables:
-
Java
@PlanningEntity
public class Line {
@PlanningVariable
private Operator operator;
@PlanningListVariable
private List<Job> jobs;
...
}The mixed models also allow for the creation of multiple planning entities, each defining its own variables:
-
Java
@PlanningEntity
public class Line {
@PlanningListVariable
private List<Job> jobs;
...
}
@PlanningEntity
public class LineOperation {
@PlanningVariable
private Operator operator;
...
}|
Creating mixed models with chained and list variables is prohibited, and only one list variable can be defined. |
9. Shadow variables
A shadow variable is a planning variable whose correct value can be deduced from the state of the genuine planning variables. Timefold Solver effectively only optimizes the genuine variables, and it assures that when a genuine variable changes, any dependent shadow variables are changed accordingly.
Shadow variables can be defined by:
-
Using one of the built-in shadow variable annotations;
-
Defining them yourselves using custom shadow variables.
9.1. Built-in shadow variables
Timefold Solver provides various built-in shadow variable annotation that make configuring common shadow variables trivial. Their applicability and usage varies depending on your use of @PlanningVariable, @PlanningListVariable or the chained @PlanningVariable
Detailed information on these built-in shadow variables can be found in the section on shadow variables of each of the genuine variable variants:
9.2. Custom Shadow Variables
Custom shadow variables can be used to derive values of shadow variables from genuine variables or other shadow variables. This approach allows access to all the fields and methods of the declaring class.
To define a declarative shadow variable: Annotate the field with @ShadowVariable and specify the name of a supplier method.
Annotate the supplier method with @ShadowSources, listing all the planning variables (genuine or shadow) it depends on.
Whenever any of the declared sources change, the supplier method is invoked, and its return value is set on all fields that reference it via @ShadowVariable.
-
Java
@PlanningEntity
public class Job {
@PlanningVariable
private LocalDate startDate;
private int durationInDays;
@ShadowVariable(supplierName="endDateSupplier")
private LocalDate endDate;
@ShadowSources("startDate")
public LocalDate endDateSupplier() {
if (startDate == null) {
return null;
} else {
return startDate.plusDays(durationInDays);
}
}
}In the example above, whenever the solver changes the startDate planning variable, the endDateSupplier() method is called.
Its return value is assigned to the endDate field, as declared by the @ShadowVariable(supplierName="endDateSupplier") annotation.
Some key considerations:
-
Type consistency: The return type of the supplier method must match the type of the field it is assigned to.
-
Explicit dependencies: All planning variables used in the supplier logic must be explicitly listed in
@ShadowSources. Undeclared dependencies will not trigger updates, leading to stale or incorrect shadow values.
9.2.1. @ShadowSources paths
When using @ShadowSources, you must specify the paths to the variables that the supplier method depends on to compute its value.
These paths must follow 1 of 3 syntactic forms:
| Form | Syntax Example | Description |
|---|---|---|
Simple Variable Name |
"variableName" |
Refers to a variable (genuine or shadow) on the same planning entity. |
Chained Property Path |
"a.b.c" |
Refers to a variable reachable via chained properties. Intermediate elements must be facts or variables; the final one must be a variable. |
Collection Element Access |
"collectionVar[].varName" |
Refers to a variable ( |
Let’s illustrate this with a specific example.
-
Java
@PlanningEntity
public class Job {
@PreviousElementShadowVariable
Job previous;
private int durationInDays;
private Collection<Job> dependencies;
@ShadowVariable(supplierName="startDateSupplier")
private LocalDateTime startDate;
@ShadowVariable(supplierName="endDateSupplier")
private LocalDate endDate;
@ShadowSources({"previous.endDate", "dependencies[].endDate"})
public LocalDate startDateSupplier() {
LocalDate readyDate = null;
if (previous != null) {
readyDate = previous.endDate;
} else {
return null;
}
if (dependencies != null) {
for (var dependency : dependencies) {
if (dependency.endDate == null) {
return null;
}
if (readyDate.isBefore(dependency.endDate)) {
readyDate = dependency.endDate;
}
}
}
return readyDate;
}
@ShadowSources("startDate")
public LocalDate endDateSupplier() {
if (startDate == null) {
return null;
} else {
return startDate.plusDays(durationInDays);
}
}
}| Reference | Form | Meaning |
|---|---|---|
"startDate" |
Simple Variable Name |
Direct reference to the |
"previous.endDate" |
Chained Property Path |
Accesses |
"dependencies[].endDate" |
Collection Element Access |
Accesses |
9.2.2. Detecting Inconsistencies in Shadow Variables
In certain cases, shadow variables may form an infinite loop. There are three ways a loop can form:
-
Source-induced, when two custom shadow variables' sources refer to each other:
-
Java
@PlanningEntity public class Entity { @ShadowVariable(supplierName="variable1Supplier") String variable1; @ShadowVariable(supplierName="variable2Supplier") String variable2; // ... @ShadowSources("variable2") String variable1Supplier() { /* ... */ } @ShadowSources("variable1") String variable2Supplier() { /* ... */ } } -
-
Fact-induced, when a shadow variable has itself as a direct or transitive dependency via a fact:
-
Java
@PlanningEntity public class Entity { Entity dependency; @ShadowVariable(supplierName="variableSupplier") String variable; @ShadowSources("dependency.variable") String variableSupplier() { /* ... */ } // ... } Entity a = new Entity(); Entity b = new Entity(); a.setDependency(b); b.setDependency(a); // a depends on b, and b depends on a, which is invalid. -
-
Variable-induced, when a shadow variable has itself as a direct or transitive dependency via a variable:
-
Java
@PlanningEntity public class Entity { Entity dependency; @PreviousElementShadowVariable(/* ... */) Entity previous; @ShadowVariable(supplierName="variableSupplier") String variable; @ShadowSources({"previous.variable", "dependency.variable"}) String variable1Supplier() { /* ... */ } // ... } Entity a = new Entity(); Entity b = new Entity(); b.setDependency(a); a.setPrevious(b); // b depends on a via a fact, and a depends on b via a variable // The solver can break this loop by moving a after b. -
|
Source-induced and fact-induced loops cannot be broken by the solver, and represents an issue in either the input problem or the domain model. The solver will fail-fast if it detects a source-induced or fact-induced loop. |
A declarative shadow variable is considered inconsistent if:
-
It is part of a loop. For example, if variable
adepends onbandbdepends ona, both are in a loop. -
It depends on another variable that is inconsistent. For example, if
cdepends ona, andais in a loop withb, thencis also considered part of the loop.
When a declarative shadow variable is inconsistent, it will be set to null.
To detect whether an entity has inconsistent shadow variables, annotate a boolean field with @ShadowVariablesInconsistent.
The solver will set this field to true if the entity has any inconsistent shadow variables.
-
Java
@PlanningEntity
public class Job {
@ShadowVariablesInconsistent
boolean isInconsistent;
public boolean isInconsistent() {
return isInconsistent;
}
}
@ShadowSources-annotated methods do not need to check @ShadowVariablesInconsistent-annotated properties.
These methods are only called if none of their shadow variables are inconsistent, and therefore the value of such properties at that time is guaranteed to be false.
|
This property (isInconsistent in the example above) is typically used in a constraint filter to penalize entities with inconsistent shadow variables via a hard constraint, since PlanningSolution instances containing inconsistent shadow variables are generally considered invalid.
-
Java
//Example constraint
Constraint penalizeInconsistentJobs(ConstraintFactory factory) {
return factory.forEachUnfiltered(Job.class)
.filter(job -> job.isInconsistent())
.penalize(HardSoftScore.ONE_HARD)
.asConstraint("Job has inconsistent shadow variables.");
}
Since forEach filters out inconsistent entities, you must use forEachUnfiltered to penalize inconsistent entities.
|
9.2.3. Aligning Shadow Variables
@ShadowSources has an optional alignmentKey parameter that can be used to reuse calculation results to increase performance.
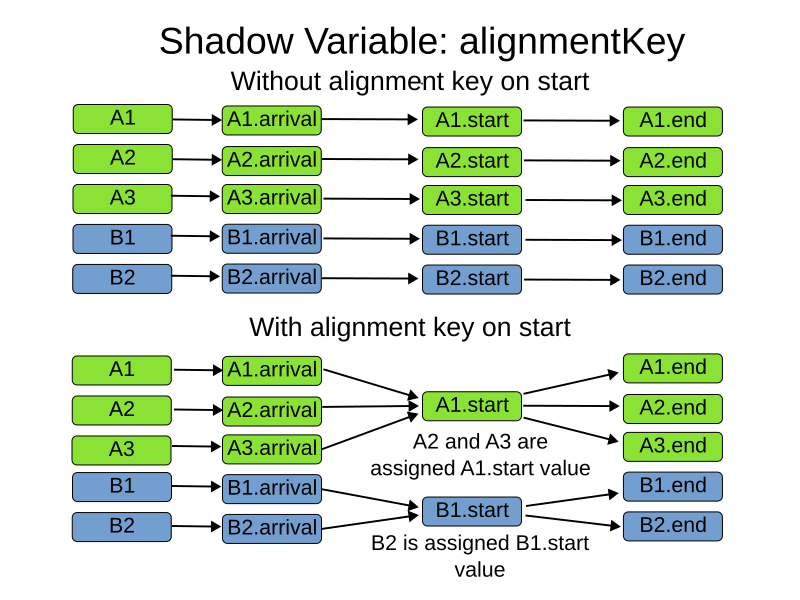
To be used, a few requirements must be met:
-
alignmentKeymust reference a property that remains constant during solving. It may point to a problem fact, planning entity or a regular property of the planning entity, but it cannot reference any planning variables. -
For all entities with the same, non-null
alignmentKeyvalue, calling the supplier method must result in the same value regardless of what entity is called.
|
Only use alignment keys when you can guarantee the two requirements above are met. Since the calculation will only be performed on a single entity, if the supplier method can return a different value depending on what aligned entity is chosen, you will get inconsistent and incorrect results. |
The code below meets the requirements, since the leader field is not a variable, and entities with the same leader will get the same value.
-
Java
@PlanningEntity
public class Leader {
@PlanningVariable
Integer value;
// ...
}
@PlanningEntity
public class Follower {
Leader leader;
@ShadowVariable(supplierName="valueSupplier")
Integer value;
@ShadowSources(value = {"leader.value"}, alignmentKey = "leader")
public Integer valueSupplier() {
return leader.value;
}
}However, the code below does not meet the requirements, since Follower entities with the same leader but a different minValue may calculate different values.
-
Java
@PlanningEntity
public class Leader {
@PlanningVariable
Integer value;
// ...
}
@PlanningEntity
public class Follower {
Leader leader;
int minValue;
@ShadowVariable(supplierName="valueSupplier")
Integer value;
@ShadowSources(value = {"leader.value"}, alignmentKey = "leader")
public Integer valueSupplier() {
if (leader.value == null || leader.value < minValue) {
return minValue;
}
return leader.value;
}
}Entities where the alignmentKey is evaluated to null are each calculated separately and won’t share calculations for that shadow variable with other entities.
This feature is particularly useful when you have a group of entities that must be aligned to the same value. For example:
-
Java
@PlanningEntity
public class Job {
@PreviousElementShadowVariable
Job previous;
private Collection<Job> alignedJobs;
@ShadowVariable(supplierName="readyDateSupplier")
private LocalDateTime readyDate;
@ShadowVariable(supplierName="startDateSupplier")
private LocalDateTime startDate;
@ShadowSources(/* ... */)
public LocalDate readyDateSupplier() {
// ...
}
@ShadowSources(value = {"readyDate", "alignedJobs[].readyDate"}, alignmentKey="alignedJobs")
public LocalDate startDateSupplier() {
if (alignedJobs == null) {
// All entities with a null alignmentKey (in this case, "alignedJobs")
// are calculated separately.
return readyDate;
}
var lastReadyDate = readyDate;
for (var job : alignedJobs) {
if (job.readyDate.isAfter(lastReadyDate)) {
lastReadyDate = job.readyDate;
}
}
return lastReadyDate;
}
}9.2.4. Optimizing Shadow Variables
Each custom Shadow Variable on each planning entity constitutes one node of a reference graph. The Solver analyzes this graph to decide what is the most optimal strategy for updating these variables. In general, the less variables and the less dependencies between them, the faster the processing. For the best performance, follow these guidelines:
-
Keep all custom Shadow Variables on the same entity class. If one entity is grouping another entity, you might be able to use custom Shadow Variable alignment to keep custom Shadow Variables on the same entity class.
-
Do not use both
@PreviousElementShadowVariableand@NextElementShadowVariablein your sources. This includes using@PreviousElementShadowVariableas a source in one custom Shadow Variable while using@NextElementShadowVariableas a source in another custom Shadow Variable. -
Compute as much as possible within a single custom Shadow Variable supplier method. Do not create intermediate custom Shadow Variables when it is possible to compute the value directly from another custom Shadow Variable.
| These are tips and tricks for optimal performance and needn’t be followed to the letter. The solver will work correctly even if you decide not to follow any of the advice, albeit with slightly lesser performance. |
9.3. Custom VariableListener
|
Deprecation notice: Using |
To update a shadow variable, Timefold Solver uses a VariableListener.
To define a custom shadow variable, write a custom VariableListener:
implement the interface and annotate it on the shadow variable that needs to change.
-
Java
@PlanningVariable(...)
public Standstill getPreviousStandstill() {
return previousStandstill;
}
@ShadowVariable(
variableListenerClass = VehicleUpdatingVariableListener.class,
sourceVariableName = "previousStandstill")
public Vehicle getVehicle() {
return vehicle;
}Register this class as a planning entity if it isn’t already. Otherwise Timefold Solver won’t detect it and the shadow variable won’t update.
The sourceVariableName is the (genuine or shadow) variable that triggers changes to the annotated shadow variable.
If the source variable is declared on a different class than the annotated shadow variable’s class,
also specify the sourceEntityClass and make sure the shadow variable’s class is registered as a planning entity.
Implement the VariableListener interface.
For example, the VehicleUpdatingVariableListener assures that every Customer in a chain has the same Vehicle, namely the chain’s anchor.
-
Java
public class VehicleUpdatingVariableListener implements VariableListener<VehicleRoutePlan, Customer> {
public void afterEntityAdded(ScoreDirector<VehicleRoutePlan> scoreDirector, Visit customer) {
updateVehicle(scoreDirector, customer);
}
public void afterVariableChanged(ScoreDirector<VehicleRoutePlan> scoreDirector, Visit customer) {
updateVehicle(scoreDirector, customer);
}
...
protected void updateVehicle(ScoreDirector<VehicleRoutePlan> scoreDirector, Visit sourceCustomer) {
Standstill previousStandstill = sourceCustomer.getPreviousStandstill();
Vehicle vehicle = previousStandstill == null ? null : previousStandstill.getVehicle();
Visit shadowCustomer = sourceCustomer;
while (shadowCustomer != null && shadowCustomer.getVehicle() != vehicle) {
scoreDirector.beforeVariableChanged(shadowCustomer, "vehicle");
shadowCustomer.setVehicle(vehicle);
scoreDirector.afterVariableChanged(shadowCustomer, "vehicle");
shadowCustomer = shadowCustomer.getNextCustomer();
}
}
}|
A |
|
Any change of a shadow variable must be told to the |
9.3.1. Multiple source variables
If your custom variable listener needs multiple source variables to compute the shadow variable, annotate the shadow variable with multiple @ShadowVariable annotations, one per each source variable.
-
Java
@PlanningVariable(...)
public ExecutionMode getExecutionMode() {
return executionMode;
}
@PlanningVariable(...)
public Integer getDelay() {
return delay;
}
@ShadowVariable(
variableListenerClass = PredecessorsDoneDateUpdatingVariableListener.class,
sourceVariableName = "executionMode")
@ShadowVariable(
variableListenerClass = PredecessorsDoneDateUpdatingVariableListener.class,
sourceVariableName = "delay")
public Integer getPredecessorsDoneDate() {
return predecessorsDoneDate;
}9.3.2. Piggyback shadow variable
If one VariableListener changes two or more shadow variables (because having two separate VariableListeners would be inefficient), then annotate only the first shadow variable with @ShadowVariable and specify the variableListenerClass there.
Use @PiggybackShadowVariable on each shadow variable updated by that variable listener and reference the first shadow variable:
-
Java
@PlanningVariable(...)
public Standstill getPreviousStandstill() {
return previousStandstill;
}
@ShadowVariable(
variableListenerClass = TransportTimeAndCapacityUpdatingVariableListener.class,
sourceVariableName = "previousStandstill")
public Integer getTransportTime() {
return transportTime;
}
@PiggybackShadowVariable(shadowVariableName = "transportTime")
public Integer getCapacity() {
return capacity;
}9.3.3. VariableListener triggering order
All shadow variables are triggered by a VariableListener, regardless if it’s a built-in or a custom shadow variable.
The genuine and shadow variables form a graph, that determines the order in which the afterEntityAdded(), afterVariableChanged() and afterEntityRemoved() methods are called:
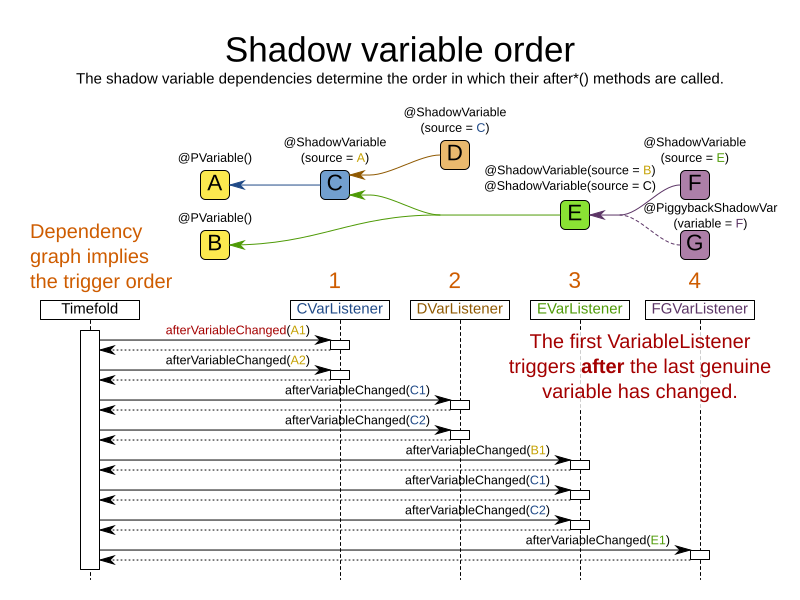
|
In the example above, D could have also been ordered after E (or F) because there is no direct or indirect dependency between D and E (or F). |
Timefold Solver guarantees that:
-
The first
VariableListener'safter*()methods trigger after the last genuine variable has changed. Therefore the genuine variables (A and B in the example above) are guaranteed to be in a consistent state across all its instances (with values A1, A2 and B1 in the example above) because the entireMovehas been applied. -
The second
VariableListener'safter*()methods trigger after the last first shadow variable has changed. Therefore the first shadow variable (C in the example above) are guaranteed to be in a consistent state across all its instances (with values C1 and C2 in the example above). And the genuine variables too. -
And so forth.
Timefold Solver does not guarantee the order in which the after*() methods are called for the sameVariableListener with different parameters (such as A1 and A2 in the example above), although they are likely to be in the order in which they were affected.
By default, Timefold Solver does not guarantee that the events are unique.
For example, if a shadow variable on an entity is changed twice in the same move (for example by two different genuine variables), then that will cause the same event twice on the VariableListeners that are listening to that original shadow variable.
To avoid dealing with that complexity, overwrite the method requiresUniqueEntityEvents() to receive unique events at the cost of a small performance penalty:
-
Java
public class StartTimeUpdatingVariableListener implements VariableListener<TaskAssigningSolution, Task> {
@Override
public boolean requiresUniqueEntityEvents() {
return true;
}
...
}9.4. Shadow variable cloning
A shadow variable’s value (just like a genuine variable’s value)
isn’t planning cloned by the default solution cloner,
unless it can easily prove that it must be planning cloned (for example the property type is a planning entity class).
Specifically shadow variables of type List, Set, Collection or Map usually need to be planning cloned
to avoid corrupting the best solution when the working solution changes.
To planning clone a shadow variable, add @DeepPlanningClone annotation:
-
Java
@DeepPlanningClone
@ShadowVariable(...)
private Map<LocalDateTime, Integer> usedManHoursPerDayMap;9.5. Testing a shadow variable
Testing the logic of shadow variables is crucial for maintaining consistency and preventing issues such as score corruption. The Timefold Solver API includes a facility method that automatically updates shadow variables from a given model, allowing you to create unit tests easily. Consider the following solution class:
-
Java
public class Schedule {
@PlanningEntityCollectionProperty
private List<Job> jobs;
...
}Next, let’s reuse the following model from previous section.
-
Java
public class Job {
public Job(LocalDate startDate, int durationInDays) {
...
}
@PlanningVariable
private LocalDate startDate;
private int durationInDays;
@ShadowVariable(supplierName="endDateSupplier")
private LocalDate endDate;
@ShadowSources("startDate")
public LocalDate endDateSupplier() {
if (startDate == null) {
return null;
} else {
return startDate.plusDays(durationInDays);
}
}
}Finally, let’s create a unit test that will validate the defined shadow variable endDate.
The utility method SolutionManager::updateShadowVariables reads the entity and updates its shadow variables.
Notably, the method updateShadowVariables simplifies the logic and does not require proper solver configuration to update the shadow variables.
-
Java
@Test
void updateShadowVariables() {
var job = new Job(LocalDate.now(), 10);
SolutionManager.updateShadowVariables(Schedule.class, job);
assertThat(job.getEndDate()).isEqualTo(LocalDate.now().plusDays(10));
}It is also possible to pass a solution instance rather than the solution class along with the related planning entities.
-
Java
@Test
void updateShadowVariables() {
var solution = new Schedule();
var job = new Job(LocalDate.now(), 10);
solution.setJobs(List.of(job));
SolutionManager.updateShadowVariables(solution);
assertThat(job.getEndDate()).isEqualTo(LocalDate.now().plusDays(10));
}|
Models using custom variable listeners are not compatible with |
In the following example, a model that uses a planning list variable is employed to demonstrate the test feature.
-
Java
public class VehicleRoutePlan {
@PlanningEntityCollectionProperty
private List<Vehicle> vehicles;
...
}The planning entity:
-
Java
@PlanningEntity
public class Vehicle {
@PlanningListVariable
List<Customer> customers;
...
}On the element side:
-
Java
@PlanningEntity
public class Customer {
@PreviousElementShadowVariable(sourceVariableName = "customers")
Customer previousCustomer;
@NextElementShadowVariable(sourceVariableName = "customers")
Customer nextCustomer;
...
}The test is defined as follows:
-
Java
void updateShadowVariables() {
var vehicle = new Vehicle();
var customer1 = new Customer();
var customer2 = new Customer();
vehicle.setCustomers(List.of(customer1, customer2));
SolutionManager.updateShadowVariables(VehicleRoutePlan.class, vehicle, customer1, customer2);
assertThat(customer1.previousCustomer).isNull();
assertThat(customer1.nextCustomer).isSameAs(customer2);
assertThat(customer2.previousCustomer).isSameAs(customer1);
assertThat(customer2.nextCustomer).isNull();
}|
In the example above, only two types of shadow variables are used, but it is not limited to these variable types.
The method |
10. Planning problem and planning solution
10.1. Planning problem instance
A dataset for a planning problem needs to be wrapped in a class for the Solver to solve.
That solution class represents both the planning problem and (if solved) a solution.
It is annotated with a @PlanningSolution annotation.
In school timetabling,
the solution class is the Timetable class, which contains a Timeslot list, a Room list, and a Lesson list.
A planning problem is actually an unsolved planning solution or - stated differently - an uninitialized solution.
In school timetabling, that Timetable class has the @PlanningSolution annotation,
yet every Lesson in an unsolved Timetable class is not yet assigned to a Timeslot (their timeslot property is null).
That’s not a feasible solution.
It’s not even a possible solution.
It’s an uninitialized solution.
10.2. Solution class
A solution class holds all problem facts, planning entities and a score.
It is annotated with a @PlanningSolution annotation.
For example, an Timetable instance holds a list of all timeslots, all rooms and all Lesson instances:
-
Java
@PlanningSolution
public class Timetable {
private String name;
// Problem facts
private List<Timeslot> timeslots;
private List<Room> rooms;
// Planning entities
private List<Lesson> lessons;
private HardSoftScore score;
...
}The solver configuration needs to declare the planning solution class:
<solver xmlns="https://timefold.ai/xsd/solver" xmlns:xsi="http://www.w3.org/2001/XMLSchema-instance"
xsi:schemaLocation="https://timefold.ai/xsd/solver https://timefold.ai/xsd/solver/solver.xsd">
...
<solutionClass>org.acme.schooltimetabling.Timetable</solutionClass>
...
</solver>|
Solution class must not be of Java’s |
10.3. Planning entities of a solution (@PlanningEntityCollectionProperty)
Timefold Solver needs to extract the entity instances from the solution instance.
It gets those collection(s) by calling every getter (or field) that is annotated with @PlanningEntityCollectionProperty:
-
Java
@PlanningSolution
public class Timetable {
...
private List<Lesson> lessons;
@PlanningEntityCollectionProperty
public List<Lesson> getLessons() {
return lessons;
}
}There can be multiple @PlanningEntityCollectionProperty annotated members.
Those can even return a Collection with the same entity class type.
Instead of Collection, it can also return an array.
|
A |
In rare cases, a planning entity might be a singleton: use @PlanningEntityProperty on its getter (or field) instead.
Both annotations can also be auto discovered if enabled.
10.4. Score of a Solution (@PlanningScore)
A @PlanningSolution class requires a score property (or field), which is annotated with a @PlanningScore annotation.
The score property is null if the score hasn’t been calculated yet.
The score property is typed to the specific Score implementation of your use case.
Most use cases use a HardSoftScore:
-
Java
@PlanningSolution
public class Timetable {
...
@PlanningScore
private HardSoftScore score;
@PlanningScore
public HardSoftScore getScore() {
return score;
}
public void setScore(HardSoftScore score) {
this.score = score;
}
...
}Some use cases use other score types.
This annotation can also be auto discovered if enabled.
10.5. Problem facts of a solution (@ProblemFactCollectionProperty)
For Constraint Streams,
Timefold Solver needs to extract the problem fact instances from the solution instance.
It gets those collection(s) by calling every method (or field) that is annotated with @ProblemFactCollectionProperty.
All objects returned by those methods are available to use by Constraint Streams.
For example, in Timetable all Timeslot and Room instances are problem facts.
-
Java
@PlanningSolution
public class Timetable {
...
@ProblemFactCollectionProperty
@ValueRangeProvider
private List<Timeslot> timeslots;
@ProblemFactCollectionProperty
@ValueRangeProvider
private List<Room> rooms;
...
}All planning entities are automatically inserted into the working memory. Do not add an annotation on their properties.
|
The problem facts methods are not called often: at most only once per solver phase per solver thread. |
There can be multiple @ProblemFactCollectionProperty annotated members.
Those can even return a Collection with the same class type, but they shouldn’t return the same instance twice.
Instead of Collection, it can also return an array.
|
A @ProblemFactCollectionProperty annotation needs to be on a member in a class with a @PlanningSolution annotation. It is ignored on parent classes or subclasses without that annotation. |
In rare cases, a problem fact might be a singleton: use @ProblemFactProperty on its method (or field) instead.
Both annotations can also be auto discovered if enabled.
10.5.1. Cached problem fact
A cached problem fact is a problem fact that does not exist in the real domain model,
but is calculated before the Solver really starts solving.
The problem facts methods have the opportunity to enrich the domain model with such cached problem facts,
which can lead to simpler and faster score constraints.
For example, in examination, a cached problem fact TopicConflict is created for every two Topics which share at least one Student.
-
Java
@ProblemFactCollectionProperty
private List<TopicConflict> calculateTopicConflictList() {
List<TopicConflict> topicConflictList = new ArrayList<TopicConflict>();
for (Topic leftTopic : topicList) {
for (Topic rightTopic : topicList) {
if (leftTopic.getId() < rightTopic.getId()) {
int studentSize = 0;
for (Student student : leftTopic.getStudentList()) {
if (rightTopic.getStudentList().contains(student)) {
studentSize++;
}
}
if (studentSize > 0) {
topicConflictList.add(new TopicConflict(leftTopic, rightTopic, studentSize));
}
}
}
}
return topicConflictList;
}Where a score constraint needs to check that no two exams with a topic that shares a student are scheduled close together
(depending on the constraint: at the same time, in a row, or in the same day),
the TopicConflict instance can be used as a problem fact, rather than having to combine every two Student instances.
10.6. Auto discover solution properties
Instead of configuring each property (or field) annotation explicitly, some can also be deduced automatically by Timefold Solver:
@PlanningSolution(autoDiscoverMemberType = AutoDiscoverMemberType.FIELD)
public class VehicleRoutePlan {
...
}The AutoDiscoverMemberType can be:
-
NONE: No auto discovery. -
FIELD: Auto discover all fields on the@PlanningSolutionclass -
GETTER: Auto discover all getters on the@PlanningSolutionclass
The automatic annotation is based on the field type (or getter return type):
-
@ProblemFactProperty: when it isn’t aCollection, an array, a@PlanningEntityclass or aScore -
@ProblemFactCollectionProperty: when it’s aCollection(or array) of a type that isn’t a@PlanningEntityclass -
@PlanningEntityProperty: when it is a configured@PlanningEntityclass or subclass -
@PlanningEntityCollectionProperty: when it’s aCollection(or array) of a type that is a configured@PlanningEntityclass or subclass -
@PlanningScore: when it is aScoreor subclass
These automatic annotations can still be overwritten per field (or getter).
Specifically, a BendableScore always needs to override
with an explicit @PlanningScore annotation to define the number of hard and soft levels.
10.7. Cloning a solution
Most (if not all) optimization algorithms clone the solution each time they encounter a new best solution (so they can recall it later) or to work with multiple solutions in parallel.
|
There are many ways to clone, such as a shallow clone, deep clone, … This context focuses on a planning clone. |
A planning clone of a solution must fulfill these requirements:
-
The clone must represent the same planning problem. Usually it reuses the same instances of the problem facts and problem fact collections as the original.
-
The clone must use different, cloned instances of the entities and entity collections. Changes to an original solution entity’s variables must not affect its clone.
Implementing a planning clone method is hard, therefore you do not need to implement it.
10.7.1. FieldAccessingSolutionCloner
This SolutionCloner is used by default.
It works well for most use cases.
|
When the |
The FieldAccessingSolutionCloner does not clone problem facts by default.
If any of your problem facts needs to be deep cloned for a planning clone,
for example if the problem fact references a planning entity or the planning solution,
mark its class with a @DeepPlanningClone annotation:
-
Java
@DeepPlanningClone
public class SeatDesignationDependency {
private SeatDesignation leftSeatDesignation; // planning entity
private SeatDesignation rightSeatDesignation; // planning entity
...
}In the example above, because SeatDesignationDependency references the planning entity SeatDesignation
(which is deep planning cloned automatically), it should also be deep planning cloned.
Alternatively, the @DeepPlanningClone annotation also works on a getter method or a field to planning clone it.
If that property is a Collection or a Map, it will shallow clone it and deep planning clone
any element thereof that is an instance of a class that has a @DeepPlanningClone annotation.
-
Java
@DeepPlanningClone
private SeatDesignationDependency seatDesignationDependency;|
Values of Java’s |
10.7.2. Custom cloning with a SolutionCloner
To use a custom cloner, configure it on the planning solution:
@PlanningSolution(solutionCloner = TimetableSolutionCloner.class)
public class Timetable {
...
}For example, a Timetable planning clone only deep clones all Timetable instances.
So when the original solution changes (later on during planning) and one or more Timetable instances change,
the planning clone isn’t affected.
The cloneSolution() method should only deep clone the planning entities.
The problem facts, such as Timeslot and Room are normally not cloned: even their List instances are not cloned.
If the problem facts were cloned too,
then you would have to make sure that the new planning entity clones also refer to the new problem facts clones used by the cloned solution.
For example, if you were to clone all Timeslot instances,
then each Lesson clone and the Timetable clone itself should refer to those new Timeslot clones.
|
Cloning an entity with a chained variable is devious: a variable of an entity A might point to another entity B. If A is cloned, then its variable must point to the clone of B, not the original B. |
10.8. Create an uninitialized solution
Create a @PlanningSolution instance to represent your planning problem’s dataset, so it can be set on the Solver as the planning problem to solve.
In school timetabling, a Timetable instance is created with the required Room and Timeslot instances
and every Lesson has its planning variables set to null:
-
Java
public static Timetable generateDemoData(DemoData demoData) {
List<Timeslot> timeslots = new ArrayList<>(10);
long nextTimeslotId = 0L;
timeslots.add(new Timeslot(Long.toString(nextTimeslotId++), DayOfWeek.MONDAY, LocalTime.of(8, 30), LocalTime.of(9, 30)));
timeslots.add(new Timeslot(Long.toString(nextTimeslotId++), DayOfWeek.MONDAY, LocalTime.of(9, 30), LocalTime.of(10, 30)));
timeslots.add(new Timeslot(Long.toString(nextTimeslotId++), DayOfWeek.MONDAY, LocalTime.of(10, 30), LocalTime.of(11, 30)));
timeslots.add(new Timeslot(Long.toString(nextTimeslotId++), DayOfWeek.MONDAY, LocalTime.of(13, 30), LocalTime.of(14, 30)));
timeslots.add(new Timeslot(Long.toString(nextTimeslotId++), DayOfWeek.MONDAY, LocalTime.of(14, 30), LocalTime.of(15, 30)));
...
List<Room> rooms = new ArrayList<>(3);
long nextRoomId = 0L;
rooms.add(new Room(Long.toString(nextRoomId++), "Room A"));
rooms.add(new Room(Long.toString(nextRoomId++), "Room B"));
rooms.add(new Room(Long.toString(nextRoomId++), "Room C"));
List<Lesson> lessons = new ArrayList<>();
long nextLessonId = 0L;
lessons.add(new Lesson(Long.toString(nextLessonId++), "Math", "A. Turing", "9th grade"));
lessons.add(new Lesson(Long.toString(nextLessonId++), "Math", "A. Turing", "9th grade"));
lessons.add(new Lesson(Long.toString(nextLessonId++), "Physics", "M. Curie", "9th grade"));
lessons.add(new Lesson(Long.toString(nextLessonId++), "Chemistry", "M. Curie", "9th grade"));
lessons.add(new Lesson(Long.toString(nextLessonId++), "Biology", "C. Darwin", "9th grade"));
...
return new Timetable(demoData.name(), timeslots, rooms, lessons);
}Usually, most of this data comes from your data layer, and your solution implementation just aggregates that data and creates the uninitialized planning entity instances for the solver to plan.
11. Inheritance for Planning Solutions
You can use Java’s type system naturally to model your problem. The solver however enforces some additional restrictions on how inheritance can be used when it comes planning solutions:
-
If both the child and parent solution classes are annotated, the solver must identify and accept all the defined annotated members from each class.
-
If a child class is not annotated yet inherits from a solution class, it should be considered a solution, and the previous statement continues to apply to it.
-
If a class declares any annotated members, it must be annotated as a solution, even if a supertype already has the annotation.
-
A child solution class must not redefine any existing annotated member, but it can add new ones.
-
Inheriting annotated members from more than one parent solution class, also known as multiple inheritance, is not allowed. Therefore, only one parent solution class or one level of inheritance is allowed.
11.1. Defining multiple annotated members
According to the first rule, you can define multiple annotated members through the use of inheritance.
The following example illustrates two planning solutions, where the child class ExtendedSolution inherits from BaseSolution. Additionally, multiple annotated members, valueList, entityList, score, and secondEntityList, are accessed.
-
Java
@PlanningSolution
public class BaseSolution {
@ProblemFactCollectionProperty
private List<String> valueList;
@PlanningEntityCollectionProperty
private List<? extends TestdataBothAnnotatedBaseEntity> entityList;
@PlanningScore
private SimpleScore score;
...
}
@PlanningSolution
public class ExtendedSolution extends BaseSolution {
@PlanningEntityCollectionProperty
private List<TestdataBothAnnotatedChildEntity> secondEntityList;
...
}11.2. Inheriting annotated members
Non-annotated solution classes can inherit annotated members from annotated solutions, as stated by the second rule.
In the code snippet below,
we can see that the class ExtendedSolution does not have the @PlanningSolution annotation.
However, it is still recognized as an solution class because its direct parent class is annotated.
-
Java
@PlanningSolution
public class BaseSolution {
@ProblemFactCollectionProperty
private List<String> valueList;
...
}
public class ExtendedSolution extends BaseSolution {
...
}11.3. Non-solution classes cannot define annotated members
Non-solution classes cannot define any annotated members.
The model BaseSolution includes an annotated member but lacks the @PlanningSolution annotation.
-
Java
public class BaseSolution {
@ProblemFactCollectionProperty
private List<String> valueList;
...
}
@PlanningSolution
public class ExtendedSolution extends BaseSolution {
...
}11.4. Redefining annotated members
The redefinition of annotated members through inheritance is not allowed (fourth rule).
The subsequent example illustrates that the member valueList is redefined in the child class,
which violates this rule.
-
Java
public class BaseSolution {
@ProblemFactCollectionProperty
private List<String> valueList;
...
}
@PlanningSolution
public class ExtendedSolution extends BaseSolution {
@ProblemFactCollectionProperty
private List<String> valueList;
...
}11.5. Multiple inheritance
Multiple inheritance, or inheriting properties from more than one parent solution, is not permitted. The following model demonstrates an inheritance chain with three solution classes, but it only supports a maximum of two.
-
Java
@PlanningSolution
public class BaseSolution {
...
}
@PlanningSolution
public class ChildSolution extends BaseSolution {
...
}
@PlanningSolution
public class ExtendedSolution extends ChildSolution {
...
}12. Inheritance for Planning Entities
Similar to planning solutions, there are also restrictions on the use of inheritance and modeling planning entities:
-
If both the child and parent entities are annotated, the solver must identify and accept all defined variables from each class, ensuring the solving process fills in these planning variables.
-
If a child class is not annotated yet inherits from an entity class or implements an entity interface, it should be considered an entity, and the previous statement continues to apply to it.
-
If a class declares any variable (genuine or shadow), it must be annotated as an entity, even if a supertype already has the annotation.
-
A child entity must not redefine any existing planning variable, but it can add new variables (genuine or shadow).
-
Inheriting properties from more than one parent entity, also known as multiple inheritance, is not allowed. Therefore, only one parent entity or one level of inheritance is allowed.
-
Mixing inheritance models with classes and interfaces is prohibited. Therefore, inheriting exclusively from classes or only from interfaces is acceptable.
12.1. Defining multiple planning variables
The first rule defines that multiple planning variables can be effectively modeled using inheritance.
The following example models two planning entities,
where the child class ChildEntity inherits from BaseEntity.
Additionally, two distinct planning variables, value and value2, are read.
-
Java
@PlanningEntity
public class ChildEntity extends BaseEntity {
@PlanningVariable(valueRangeProviderRefs = "valueRange2")
private String value2;
...
}
@PlanningEntity
public class BaseEntity {
@PlanningVariable(valueRangeProviderRefs = "valueRange")
private String value;
...
}The previous example can also be modeled using interfaces.
-
Java
@PlanningEntity
public class ChildEntity implements BaseEntity {
@PlanningVariable(valueRangeProviderRefs = "valueRange2")
private String value2;
...
}
@PlanningEntity
public interface BaseEntity {
@PlanningVariable(valueRangeProviderRefs = "valueRange")
String getValue();
...
}12.2. Inheriting planning variables
Non-annotated entities can inherit planning variables from annotated entities (second rule).
In the next code snippet, it can be observed that ChildEntity does not have the @PlanningEntity annotation,
but it is accepted as an entity because its direct parent is an annotated entity.
Additionally, the planning variable value will be linked with ChildEntity.
-
Java
public class ChildEntity extends BaseEntity {
...
}
@PlanningEntity
public class BaseEntity {
@PlanningVariable(valueRangeProviderRefs = "valueRange")
private String value;
...
}The use of the interface is illustrated in the following manner.
-
Java
public class ChildEntity implements BaseEntity {
...
}
@PlanningEntity
public interface BaseEntity {
@PlanningVariable(valueRangeProviderRefs = "valueRange")
String getValue();
...
}12.3. Non-entities cannot define planning variables
The third rule states that non-entities are not permitted to define planning variables.
The model BaseEntity defines a planning variable.
However, it is not marked with the @PlanningEntity annotation.
-
Java
@PlanningEntity
public class ChildEntity extends BaseEntity {
...
}
public class BaseEntity {
@PlanningVariable(valueRangeProviderRefs = "valueRange")
private String value;
...
}|
The rule also applies when the model uses interface. |
12.4. Redefining planning variables
It is not permitted to redefine planning variables when using inheritance to model your problem (fourth rule).
The following example demonstrates that the planning variable value is redefined by the child class,
which is not allowed.
-
Java
@PlanningEntity
public class ChildEntity extends BaseEntity {
@PlanningVariable(valueRangeProviderRefs = "valueRange")
private String value;
...
}
public class BaseEntity {
@PlanningVariable(valueRangeProviderRefs = "valueRange")
private String value;
...
}|
The rule also applies when the model uses interface. |
12.5. Multiple inheritance
Multiple inheritance, or inheriting properties from more than one parent entity, is not permitted. The following model illustrates an inheritance chain comprising three planning entities, but only a maximum of two are supported.
-
Java
@PlanningEntity
public class MultipleChildEntity extends ChildEntity {
...
}
@PlanningEntity
public class ChildEntity extends BaseEntity {
...
}
@PlanningEntity
public class BaseEntity {
...
}|
The rule also applies when the model uses interface. |
12.6. Mixed inheritance
It is not permitted to model inheritance using both classes and interfaces. Therefore, you can only inherit from either classes or interfaces.
-
Java
@PlanningEntity
public class MultipleChildEntity extends ChildEntity
implements BaseEntity {
...
}
@PlanningEntity
public class ChildEntity {
...
}
@PlanningEntity
public interface BaseEntity {
...
}